Sign In

JEE Advance - Physics (2019 - Paper 1 Offline - No. 11)

Two identical moving coil galvanometers have 10$$\Omega $$ resistance and full scale deflection at 2$$\mu $$A current. One of them is converted into a voltmeter of 100 mV full scale reading and the other into an ammeter of 1 mA full scale current using appropriate resistors. These are then used to measure the voltage and current in the Ohm's law experiment with R = 1000$$\Omega $$ resistor by using an ideal cell. Which of the following statement(s) is/are correct?
The resistance of the voltmeter will be 100 k$$\Omega $$.
The resistance of the ammeter will be 0.02 $$\Omega $$

(round off to 2nd decimal place).
If the ideal cell is replaced by a cell having internal resistance of 5$$\Omega $$ then the measured value of R will be more than 1000$$\Omega $$.
The measured value of R will be 978$$\Omega $$ < R < 982$$\Omega $$.

Explanation

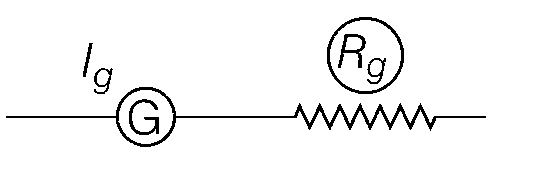
JEE Advanced 2019 Paper 1 Offline Physics - Current Electricity Question 27 English Explanation 1

$$V = 100 \times {10^{ - 3}} = {10^{ - 1}}V$$

$$V = {{\mathop{\rm l}\nolimits} _g}({R_g} + {R_v})$$

$${{{{10}^{ - 1}}} \over {2 \times {{10}^{ - 6}}}}={R_g} + {R_v}$$

$$5 \times {10^4}\Omega \approx {R_v}$$ ($$ \because $$$${R_v} < {10^5}\Omega $$)

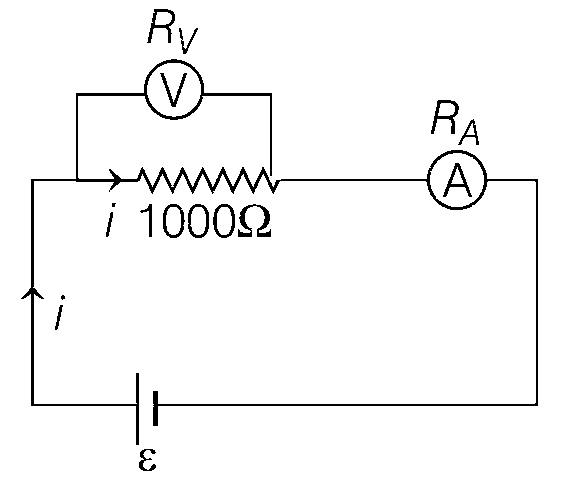
JEE Advanced 2019 Paper 1 Offline Physics - Current Electricity Question 27 English Explanation 2

IgRg = (I - Ig)S
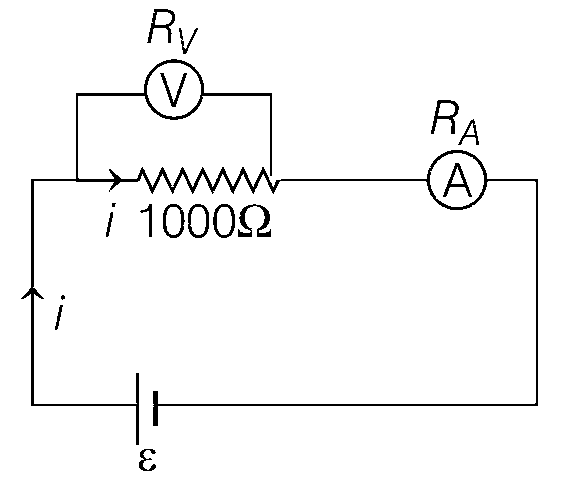
JEE Advanced 2019 Paper 1 Offline Physics - Current Electricity Question 27 English Explanation 3

$$S = {{2 \times {{10}^{ - 6}} \times 10} \over {{{10}^{ - 3}} - 2 \times {{10}^{ - 6}}}}$$

$$S = 2 \times {10^{ - 5}} \times {10^3} = 2 \times {10^{ - 2}} = 20m\Omega $$

$${R_A} = {{S{R_g}} \over {S + {R_g}}} = {{20 \times {{10}^{ - 3}} \times 10} \over {10 + 20 \times {{10}^{ - 3}}}}$$

$$ \approx 20 \times {10^{ - 3}}\Omega $$

$$i = {\varepsilon \over {\left( {{{1000 \times 50 \times {{10}^3}} \over {51 \times {{10}^3}}}} \right)}} = {{51\varepsilon } \over {5 \times {{10}^4}}}$$

($$ \because $$ RA $$ \to $$ 0)

$$i' = i\left( {{{{R_v}} \over {51 \times {{10}^3}}}} \right) = {\varepsilon \over {1000}}$$

Measured resistance,

$$ \therefore $$ $${R_m} = {{i' \times 1000} \over i} = {\varepsilon \over {51\varepsilon }} \times 5 \times 10 = 980.4\Omega $$

If the voltmeter shows full scale deflection then

$${\varepsilon \over {980}} \times \left( {{{1000} \over {51 \times {{10}^3}}}} \right) \times 5 \times {10^4} = {10^{ - 1}}$$

$$\varepsilon = 999.6$$ mV

Since, iA = 1 mA so maximum reading of R can be

$${{999.6\,mV} \over {1\,mA}} = 999.6\Omega $$

Comments (0)

Advertisement