JEE Advance - Physics (2019 - Paper 1 Offline - No. 10)
A charged shell of radius R carries a total charge Q. Given $$\phi $$ as the flux of electric field through a closed cylindrical surface of height h, radius r and with its center same as that of the shell. Here, center of the cylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Which of the following option(s) is/are correct?
[$$ \in $$0 is the permittivity of free space]
[$$ \in $$0 is the permittivity of free space]
If h > 2R and r = 4R / 5 then $$\phi $$ = Q / 5 $$ \in $$0
If h > 2R and r = 3R / 5 then $$\phi $$ = Q / 5 $$ \in $$0
If h > 8R /5 and r = 3R / 5 then $$\phi $$ = 0
If h > 2R and r = R then $$\phi $$ = Q / $$ \in $$0
Explanation
(a) h > 2R and r > R
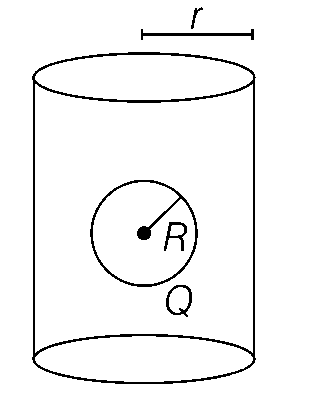
$$\phi = {Q \over {{\varepsilon _0}}}$$, clearly from Gauss' Law
(b) suppose $$h = {{8R} \over 5}$$ and $$r = {{3R} \over 5}$$
$$ \therefore $$ $$\phi $$ = 0
so, for $$h < {{8R} \over 5}$$ then $$\phi $$ = 0.
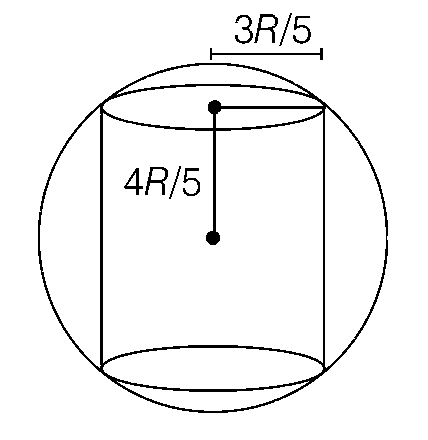
(c) For h = 3R and r = $${{4R} \over 5}$$
Shaded charge = $$2\pi (1 - \cos \,53^\circ ) \times {Q \over {4\pi }} = {Q \over 5}$$
$$ \therefore $$ $${q_{enclosed}} = {{2Q} \over 5}$$
$$ \therefore $$ $$\phi = {{2Q} \over {5{\varepsilon _0}}}$$
$$ \therefore $$ for h > 2R and $$r = {{4R} \over 5}$$
$$ \therefore $$ $$\phi = {{2Q} \over {5{\varepsilon _0}}}$$
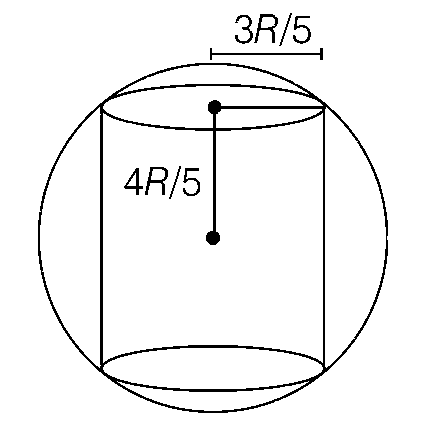
(d) like option c for h = 2R and $$r = {{3R} \over 5}$$
$${q_{enclosed}} = 2 \times 2\pi (1 - \cos \,37^\circ ){Q \over {4\pi }} = {Q \over 5}$$
$$ \therefore $$ Electric flux, $$\phi = {Q \over {5{\varepsilon _0}}}$$

$$\phi = {Q \over {{\varepsilon _0}}}$$, clearly from Gauss' Law
(b) suppose $$h = {{8R} \over 5}$$ and $$r = {{3R} \over 5}$$

$$ \therefore $$ $$\phi $$ = 0
so, for $$h < {{8R} \over 5}$$ then $$\phi $$ = 0.
(c) For h = 3R and r = $${{4R} \over 5}$$

Shaded charge = $$2\pi (1 - \cos \,53^\circ ) \times {Q \over {4\pi }} = {Q \over 5}$$
$$ \therefore $$ $${q_{enclosed}} = {{2Q} \over 5}$$
$$ \therefore $$ $$\phi = {{2Q} \over {5{\varepsilon _0}}}$$
$$ \therefore $$ for h > 2R and $$r = {{4R} \over 5}$$
$$ \therefore $$ $$\phi = {{2Q} \over {5{\varepsilon _0}}}$$
(d) like option c for h = 2R and $$r = {{3R} \over 5}$$
$${q_{enclosed}} = 2 \times 2\pi (1 - \cos \,37^\circ ){Q \over {4\pi }} = {Q \over 5}$$
$$ \therefore $$ Electric flux, $$\phi = {Q \over {5{\varepsilon _0}}}$$
Comments (0)


