JEE Advance - Physics (2018 - Paper 2 Offline - No. 7)
A solid horizontal surface is covered with a thin layer of oil. A rectangular block of mass $$m=0.4$$ $$kg$$ is at rest on this surface. An impulse of $$1.0$$ $$Ns$$ is applied to the block at time $$t=0$$ so that it starts moving along the $$x$$-axis with a velocity $$v\left( t \right) = {v_0}{e^{ - t/\tau }},$$ where $${v_0}$$ is a constant and $$\tau = 4s.$$ The displacement of the block, in metres, at $$t = \tau $$ is ______________ Take $${e^{ - 1}} = 0.37.$$
Answer
6.30
Explanation
The block was initially at rest and its velocity just after the application of impulse is $$v(0) = {v_0}{e^{ - 0/\tau }} = {v_0}$$. The applied impulse is equal to the change in linear momentum of the block i.e., J = mv0, which gives
v0 = J/m = 1/0.4 = 2.5 m/s.
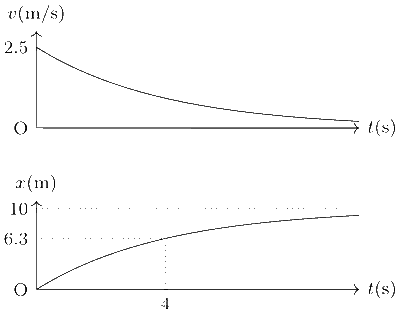
The velocity of the particle is given as
$$v(t) = {v_0}{e^{ - t/\tau }}$$.
Integrate to get the displacement
$$x(t) = \int_0^t {{v_0}{e^{ - t/\tau }}dt = {v_0}\tau (} 1 - {e^{ - t/\tau }})$$.
Substitute t = $$\tau$$ = 4 s and v0 = 2.5 m/s to get x($$\tau$$) = (2.5) (4) (1 $$-$$ e$$-$$1) = 6.3 m.
Comments (0)


