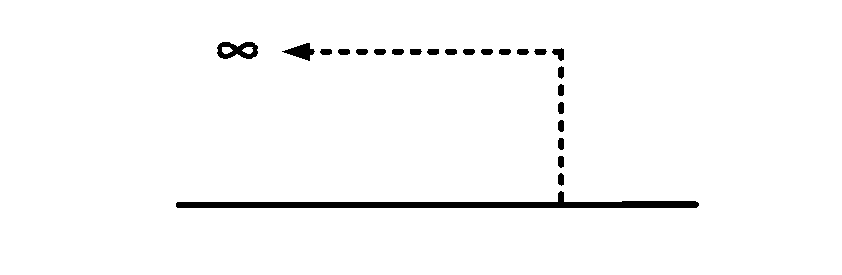
Consider the point F, the focus of the concave mirror. All rays emanating from F will be reflected back parallel to the principal axis PF. Thus, virtual image F' of the point F is formed at $$\infty$$.

Consider the point L at an object distance u = $$-$$ | f | / 2. For convenience, we use symbol $$\widehat f$$ for | f | i.e., $$\widehat f$$ = | f |. Use mirror formula, 1/v + 1/u = 1/f, with f = $$-$$ $$\widehat f$$ to get the image distance v = $$\widehat f$$. Thus, the virtual image L' of the point L is formed on the left side of the mirror at a distance $$\widehat f$$.

The image of a point on LF will lie on the line L'F'. Now, consider the point M. Its object distance is u = $$-$$ $$\widehat f$$/2. Thus, the virtual image M' of the point M is also formed at a distance $$\widehat f$$ from the mirror. The distance of M' above the principal axis is given by h_M' = $$-$$ (v/u) (LM) = $$-$$ ($$-$$2) ($$\widehat f$$/2) = $$\widehat f$$ (magnification by a spherical mirror).

Now consider a point N on the line segment FM. Let N₁ be the projection of N on the principal axis PF such that FN₁ = x. The object distance is u = $$-$$ ($$\widehat f$$ $$-$$ x). The mirror formula gives the image distance v = $$\widehat f$$ ($$\widehat f$$ $$-$$ x) / x. The distance of the image N' above the principal axis is given by h_N' = $$-$$ (v/u) (N₁N) = ($$\widehat f$$/x) (x) = $$\widehat f$$ (it is independent of x). Since, N is an arbitrary point on FM, the image of all points on FM will be formed at a distance $$\widehat f$$ above the optic axis.