JEE Advance - Physics (2018 - Paper 2 Offline - No. 15)
| LIST - I | LIST - II | ||
|---|---|---|---|
| P. | v1/v2 | 1. | 1/8 |
| Q. | L1/L2 | 2. | 1 |
| R. | K1/K2 | 3. | 2 |
| S. | T1/T2 | 4. | 8 |
Explanation
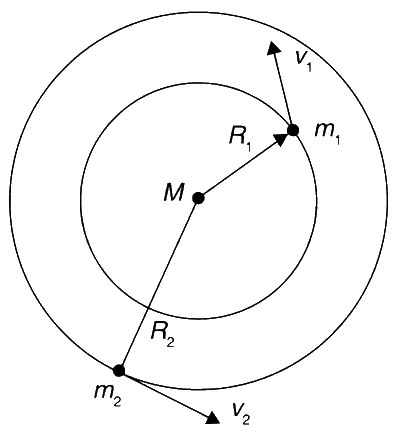
Given : $${{{m_1}} \over {{m_2}}} = 2$$ and $${{{R_1}} \over {{R_2}}} = {1 \over 4}$$
Now,
$${{GMm} \over {{R^2}}} = {{m{v^2}} \over R}$$
$$ \Rightarrow {{GM} \over R} = {v^2} \Rightarrow v = \sqrt {{{GM} \over R}} $$
$$ \Rightarrow {{{v_1}} \over {{v_2}}} = {{\sqrt {{{GM} \over {{R_1}}}} } \over {\sqrt {{{GM} \over {{R_2}}}} }} \Rightarrow {{{v_1}} \over {{v_2}}} = \sqrt {{{{R_2}} \over {{R_1}}}} $$
$$ \Rightarrow {{{v_1}} \over {{v_2}}} = \sqrt {{4 \over 1}} \Rightarrow {{{v_1}} \over {{v_2}}} = 2$$
Thus, the correct mapping is P $$\to$$ 3.
Now, L = mvR
$$ \Rightarrow {{{L_1}} \over {{L_2}}} = {{{m_1}{v_1}{R_1}} \over {{m_2}{v_2}{R_2}}} = {{{m_1}} \over {{m_2}}} \times {{{v_1}} \over {{v_2}}} \times {{{R_1}} \over {{R_2}}}$$
$$ \Rightarrow {{{L_1}} \over {{L_2}}} = 2 \times 2 \times {1 \over 4} = 1$$
Thus, the correct mapping is Q $$\to$$ 2.
Now,
$$K = {1 \over 2}m{v^2}$$
$$ \Rightarrow {{{K_1}} \over {{K_2}}} = {{{1 \over 2}{m_1}v_1^2} \over {{1 \over 2}{m_2}v_2^2}} = {{{m_1}} \over {{m_2}}} \times {\left( {{{{v_1}} \over {{v_2}}}} \right)^2}$$
$$ \Rightarrow {{{K_1}} \over {{K_2}}} = 2 \times {(2)^2} = 8$$
Thus, the correct mapping is R $$\to$$ R.
Now,
$$T = {{2\pi R} \over v}$$
$$ \Rightarrow {{{T_1}} \over {{T_2}}} = {{{{2\pi {R_1}} \over {{v_1}}}} \over {{{2\pi {R_2}} \over {{v_2}}}}} \Rightarrow {{{T_1}} \over {{T_2}}} = {{{R_1}} \over {{R_2}}} \times {{{v_2}} \over {{v_1}}}$$
$$ \Rightarrow {{{T_1}} \over {{T_2}}} = {1 \over 4} \times {1 \over 2} \Rightarrow {{{T_1}} \over {{T_2}}} = {1 \over 8}$$
Thus, the correct mapping is S $$\to$$ 1.
Therefore, option (B) is correct.
Comments (0)


