It is given that the average speed of gas molecules is u; the speed of the plate is v; the force on the plate if F.

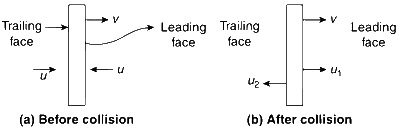
$$\bullet$$ Just before the collision : The gas molecules are approaching the leading and trailing faces of the plate with speed u.

$$\bullet$$ Just after the collision : The gas molecules bounce back with speed u₁ and u₂.

$$\bullet$$ At trailing face

The speed before collision is u $$-$$ v.

The speed after collision is u₂ + v.

From law of conservation of linear momentum, we have

u₂ + v = u $$-$$ v

That is,

u₂ = u $$-$$ 2v ....... (1)

and

$$\Delta$$u₂ = 2u $$-$$ 2v ....... (2)

$$\bullet$$ At leading face

The speed before collision is u + v.

The speed after collision is u₁ $$-$$ v.

From law of conservation of linear momentum, we have

u₁ $$-$$ v = u + v

That is,

u₁ = u + 2v ..... (3)

and

$$\Delta$$u₁ = 2u + 2v ...... (4)

Now, from Newton's second law of motion, we have

$$F = {{dp} \over {dt}}$$

$$\bullet$$ For leading face : $${F_1} = {{d{p_1}} \over {dt}}$$.

The volume swept by the plate is A(u + v). Therefore,

$${F_1} = {{d{p_1}} \over {dt}} = \rho A(u + v)\Delta {u_1}$$

$${F_1} = \rho A(u + v)(2u + 2v)$$ ....... (5)

$$\bullet$$ For trailing face : $${F_2} = {{d{p_2}} \over {dt}}$$

The volume swept by the plate is A(u $$-$$ v). Therefore,

$${F_2} = {{d{p_2}} \over {dt}} = \rho A(u - v)\Delta {u_2}$$

$${F_2} = \rho A(u - v)(2u - 2v)$$ ....... (6)

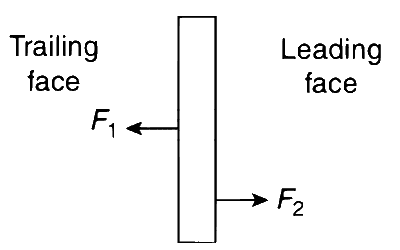
The net force on the plate is

$${F_{net}} = {F_1} - {F_2}$$

$$ = \rho A(u + v)(2u + 2v) - \rho A(u - v)(2u - 2v)$$

$$ = 2\rho A(u + v)(u + v) - 2\rho A(u - v)(u - v)$$

$$ = 2\rho A{(u + v)^2} - 2\rho A{(u - v)^2}$$

$$ = 2\rho A[{(u + v)^2} - {(u - v)^2}]$$

$$ = 2\rho A[{u^2} + {v^2} + 2uv - ({u^2} + {v^2} - 2uv)]$$

$$ = 2\rho A({u^2} + {v^2} + 2uv - {u^2} - {v^2} + 2uv)$$

$$ = 2\rho A(4uv)$$

$$ = 8\rho Auv$$

Therefore, the pressure difference is

$${{{F_{net}}} \over A} = {{8\rho Auv} \over A} = 8\rho uv$$

Thus, the pressure difference between the leading and trailing faces of the plate is proportional to uv. Hence, option (A) is correct.

Now,

$${F_{net}} = 8\rho Auv$$

The net resistive force is

$$F - (8\rho Au)v = {{mdv} \over {dt}}$$

where F is the constant force applied by the gas molecules on the plate.

The resistive force experienced by the plate is proportional to v.

Hence, option (B) is also correct.

At a later time, the velocity v becomes sufficient and the external force $$F( = 8\rho Auv)$$ balances the resistive force.

Hence, option (D) is also correct.