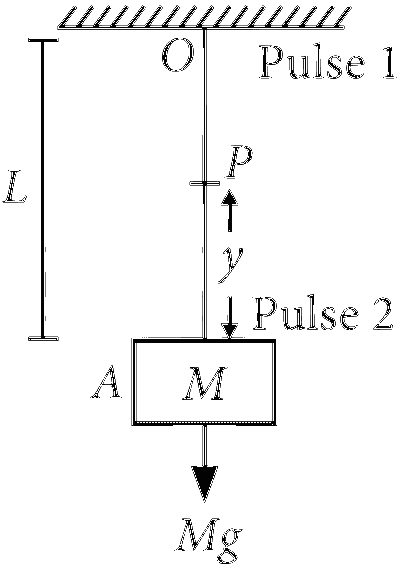
The velocity of the transverse wave is given by

$$v = \sqrt {{T \over \mu }} $$ ..... (i)

Where T is the tension in the rope and is given by

T = Mg + $$\mu$$yg

Where y = distance of point P on the rope from its bottom

L = total length of the rope

Put the value of T in eqn. (i), we get

$$v = \sqrt {{{Mg + \mu yg} \over \mu }} $$ ...... (ii)

Also, speed of pulse 1 and pulse 2 are same at each point because speed is a characteristic of the medium. Hence, speed of the two pulses are same at the mid point (x = l/2). However, since pulse 1 is moving in +x direction and pulse 2 is moving in −x direction, their velocities (which is a vector quantity) at the mid point are not same.

So, option (b) is incorrect.

Since both the pulse travel in the same medium and velocity is medium dependent. The velocity of any pulse along the rope depends on tension in the rope and linear mass density so it is independent of its frequency(characteristic of the source of pulse generation) and wavelength.

So, option (d) is correct.

Also, v = $$\nu $$$$\lambda$$ or $$\lambda$$ $$\propto$$ v

($$\because$$ frequency of a wave depends on the source)

For pulse 1, the velocity decreases at point A as tension decreases. So the wavelength of pulse 1 becomes shorter when it reaches point A.

So, option (c) is incorrect.

From eqn. (ii), the velocity is given as

$$v = \sqrt {{{Mg + \mu yg} \over \mu }} $$ or $${{dy} \over {dt}} = \sqrt {{{Mg + \mu yg} \over \mu }} \Rightarrow dt = {{dy} \over {\sqrt {{{Mg + \mu yg} \over \mu }} }}$$

Integrating both sides,

$$\int\limits_0^T {dt = \int\limits_0^L {{{dy} \over {\sqrt {{{Mg} \over \mu } + yg} }}} } $$; $$\therefore$$ $$T = {2 \over g}\left( {\sqrt {{{Mg} \over \mu } + Lg} - \sqrt {{{Mg} \over \mu }} } \right)$$

Where T is time taken by pulse to travel distance L.

Since T depends upon g, M, L and $$\mu$$ which are constant.

$$\therefore$$ Time taken by pulse 1 to reach point A and time taken by pulse 2 to reach point O is same.

$$\therefore$$ T_AO = T_OA; So option (a) is correct.