It is given that the source emits sound of frequency f₀ = 492 Hz. The car is approaching the source and the speed of car is v = 2 m/s.

Also, the speed of sound in air, v_s = 330 m/s.

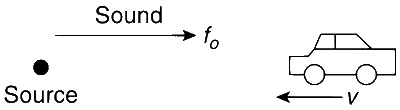
The frequency of sound received by car is given as

$${f_1} = \left( {{{{V_s} + V} \over {{V_s}}}} \right){f_0} = \left( {{{330 + 2} \over {330}}} \right)492$$

Here, f₁ = 494.98 Hz, which is the frequency reflected by the car towards the source.

Therefore, now, the car acts as the source. The frequency of sound received by the source is

$${f_2} = \left( {{{{V_s}} \over {{V_s} - v}}} \right){f_1} = \left( {{{330} \over {330 - 2}}} \right)494.98$$

Here, f₂ = 498 Hz. Therefore, the beat frequency of the resulting signal is

$$\left| {{f_0} - {f_2}} \right| = \left| {492 - 498} \right| = 6$$ Hz