JEE Advance - Physics (2016 - Paper 2 Offline - No. 9)
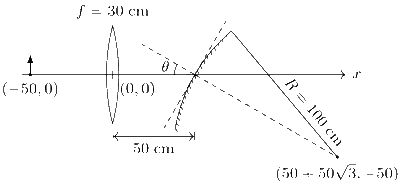
If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x, y) at which the image is formed are
Explanation
For convex lens, u = $$-$$50 cm, f = 30 cm
$$\therefore$$ $${1 \over v} = {1 \over f} + {1 \over u} = {1 \over {30}} - {1 \over {50}} = {{5 - 3} \over {150}} = {2 \over {150}}$$ or v = 75 cm
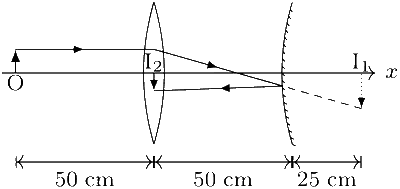
Image formed by convex lens acts as a virtual object for mirror.
If we consider that the mirror is not tilted, then for mirror,
$${u_1} = 75 - 50 = 25$$ cm, $${f_1} = {R \over 2} = {{100\,cm} \over 2} = 50$$ cm
$$\therefore$$ $${1 \over {{v_1}}} = {1 \over {{f_1}}} - {1 \over {{u_1}}} = {1 \over {50}} - {1 \over {25}} = {{ - 1} \over {50}}$$ or $${v_1} = 50$$ cm
So, the co-ordinates of final image formed (I2) if the mirror is not tilted are (0 cm, 0 cm)
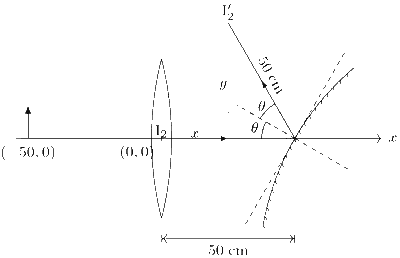
If mirror is not tilted then this ray starts from the object, refracts through the lens without deviation, incident normally on the mirror and finally comes to the image I2 after reflection from the mirror. If the mirror is tilted by an angle $$\theta$$ then this ray is incident on the mirror at an angle of reflection $$\theta$$ and finally forms a new image at I'2 (see figure). Thus, the axis on which image lies makes an angle 2$$\theta$$ = 60$$^\circ$$ with the principal axis of the lens. Also, the image distance will remain same upto the first order of approximation (image distance will remain exactly same in case of plane mirror). Thus, (x, y) coordinates of the image are
$$x = 50 - 50\cos 60^\circ = 25$$ cm,
$$y = 50\sin 60^\circ = 25\sqrt 3 $$ cm.
Comments (0)


