JEE Advance - Physics (2016 - Paper 2 Offline - No. 4)
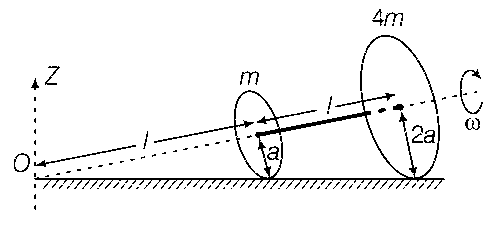
Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a
massless, rigid rod of length $$l = \sqrt {24} a$$ through their centers. This assembly is laid on a firm and flat
surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is $$\omega $$. The angular momentum of the entire assembly about the point ‘O’ is $$\overrightarrow L $$ (see the figure). Which of the following statement(s) is(are) true?

The center of mass of the assembly rotates about the z-axis with an angular speed of $${\omega \over 5}$$
The magnitude of angular momentum of center of mass of the assembly about the point O is $$81\,m{a^2}\omega $$
The magnitude of angular momentum of the assembly about its center of mass is $${{17m{a^2}\omega } \over 2}$$
The magnitude of the z-component of $$\overrightarrow L $$
is $$55m{a^2}\omega $$
Explanation
The following figure depicts the rolling condition of a circular disc:
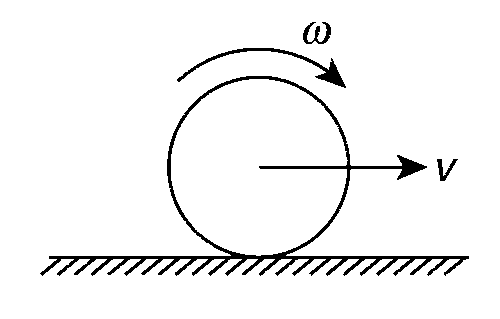
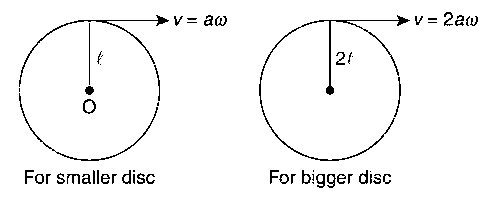
For the smaller disc, we have the velocity expressed as
v = a$$\omega$$
For the bigger disc, we have the velocity expressed as
v = (2a)$$\omega$$ = 2a$$\omega$$
Now, let us consider that both discs roll and also rotate about point O.
$$\bullet$$ The angular momentum of a rotating body is given by
$$\overrightarrow L = \overrightarrow r \times \overrightarrow p $$
About point O, the combined angular momentum of the discs is given by
L = lma$$\omega$$ + 2l(4m)(2a$$\omega$$)
where lma$$\omega$$ is due to the smaller disc and 2l(4m) (2a$$\omega$$) is due to the bigger disc.
Now, substituting the values in Eq. (1), we get
$$L = m{a^2}\omega [\sqrt {24} + 16\sqrt {24} ]$$
$$ = m{a^2}\omega (34\sqrt 6 ) \approx 83m{a^2}\omega $$
Hence, option (B) is incorrect.
$$\bullet$$ Now, let us consider that z-component of $$\overrightarrow L $$ :
$$\overrightarrow L = L\cos \theta $$
$$ = 34\sqrt 6 m{a^2}\omega \left[ {{1 \over {\sqrt {{l^2} + {a^2}} }}} \right] = 34\sqrt 6 m{a^2}\omega \left( {{{\sqrt {24} } \over 6}} \right)$$
= 81 ma2$$\omega$$
Hence, option (D) is incorrect.
$$\bullet$$ The centre of mass of the assembly about its centre of mass [i.e. the axis lavelled as (I) in the figure shown here] is
$${L_{(I)}} = {{m{a^2}} \over 2}\omega + {{4m{{(2a)}^2}} \over 2}\omega = {{17m{a^2}} \over 2}\omega $$
Hence, option (C) is correct.
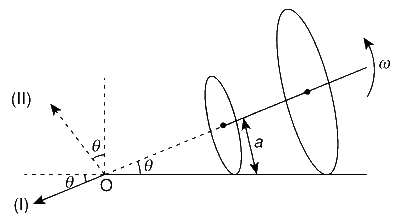
$$\bullet$$ About z-axis, the centre of mass of the assembly rotates with an angular speed
$${\omega _z} = \omega \sin \theta = \omega \left[ {{a \over {\sqrt {{l^2} + {a^2}} }}} \right] = {\omega \over 5}$$
Hence, option (A) is correct.

For the smaller disc, we have the velocity expressed as
v = a$$\omega$$
For the bigger disc, we have the velocity expressed as
v = (2a)$$\omega$$ = 2a$$\omega$$
Now, let us consider that both discs roll and also rotate about point O.

$$\bullet$$ The angular momentum of a rotating body is given by
$$\overrightarrow L = \overrightarrow r \times \overrightarrow p $$
About point O, the combined angular momentum of the discs is given by
L = lma$$\omega$$ + 2l(4m)(2a$$\omega$$)
where lma$$\omega$$ is due to the smaller disc and 2l(4m) (2a$$\omega$$) is due to the bigger disc.
Now, substituting the values in Eq. (1), we get
$$L = m{a^2}\omega [\sqrt {24} + 16\sqrt {24} ]$$
$$ = m{a^2}\omega (34\sqrt 6 ) \approx 83m{a^2}\omega $$
Hence, option (B) is incorrect.
$$\bullet$$ Now, let us consider that z-component of $$\overrightarrow L $$ :
$$\overrightarrow L = L\cos \theta $$
$$ = 34\sqrt 6 m{a^2}\omega \left[ {{1 \over {\sqrt {{l^2} + {a^2}} }}} \right] = 34\sqrt 6 m{a^2}\omega \left( {{{\sqrt {24} } \over 6}} \right)$$
= 81 ma2$$\omega$$
Hence, option (D) is incorrect.
$$\bullet$$ The centre of mass of the assembly about its centre of mass [i.e. the axis lavelled as (I) in the figure shown here] is
$${L_{(I)}} = {{m{a^2}} \over 2}\omega + {{4m{{(2a)}^2}} \over 2}\omega = {{17m{a^2}} \over 2}\omega $$
Hence, option (C) is correct.

$$\bullet$$ About z-axis, the centre of mass of the assembly rotates with an angular speed
$${\omega _z} = \omega \sin \theta = \omega \left[ {{a \over {\sqrt {{l^2} + {a^2}} }}} \right] = {\omega \over 5}$$
Hence, option (A) is correct.
Comments (0)


