JEE Advance - Physics (2016 - Paper 2 Offline - No. 3)
A gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at
pressure Pi = 105 Pa and volume Vi = 10-3 m3 changes to a final state at Pf = $$\left( {{1 \over {32}}} \right) \times {10^5}\,Pa$$ and
Vf = 8 $$ \times $$ 10-3 m3 in an adiabatic quasi-static process, such that P3V5 = constant. Consider another
thermodynamic process that brings the system from the same initial state to the same final state in two
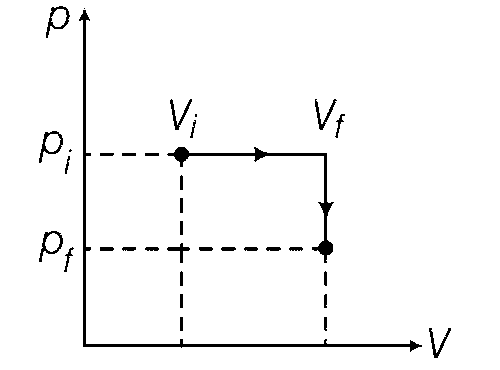
steps: an isobaric expansion at Pi followed by an isochoric (isovolumetric) process at volume Vf. The amount of heat supplied to the system in the two-step process is approximately
112 J
294 J
588 J
813 J
Explanation
In the first process : $${p_i}p_i^\gamma = {p_f}V_f^\gamma $$
$$ \Rightarrow {{{p_i}} \over {{p_f}}} = {\left( {{{{V_f}} \over {{V_i}}}} \right)^\gamma } \Rightarrow 32 = {8^\gamma }$$
$$\gamma = {5 \over 3}$$ ... (i)
For the two step process,
$$W = {p_i}({V_f} - {V_i}) = {10^5}(7 \times {10^{ - 3}})$$
$$W = 7 \times {10^2}J$$
$$\Delta U = {f \over 2}({p_f}{V_f} - {p_i}{V_i})$$
$$ = {1 \over {\gamma - 1}}\left( {{1 \over 4} \times {{10}^2} - {{10}^2}} \right)$$
$$\Delta U = - {3 \over 2}.{3 \over 4} \times {10^2} = - {9 \over 8} \times {10^2}J$$
$$Q - W = \Delta U$$
$$ \Rightarrow Q = 7 \times {10^2} - {9 \over 8} \times {10^2}$$
$$ = {{47} \over 8} \times {10^2}J = 588J$$

$$ \Rightarrow {{{p_i}} \over {{p_f}}} = {\left( {{{{V_f}} \over {{V_i}}}} \right)^\gamma } \Rightarrow 32 = {8^\gamma }$$
$$\gamma = {5 \over 3}$$ ... (i)
For the two step process,
$$W = {p_i}({V_f} - {V_i}) = {10^5}(7 \times {10^{ - 3}})$$
$$W = 7 \times {10^2}J$$
$$\Delta U = {f \over 2}({p_f}{V_f} - {p_i}{V_i})$$
$$ = {1 \over {\gamma - 1}}\left( {{1 \over 4} \times {{10}^2} - {{10}^2}} \right)$$
$$\Delta U = - {3 \over 2}.{3 \over 4} \times {10^2} = - {9 \over 8} \times {10^2}J$$
$$Q - W = \Delta U$$
$$ \Rightarrow Q = 7 \times {10^2} - {9 \over 8} \times {10^2}$$
$$ = {{47} \over 8} \times {10^2}J = 588J$$
Comments (0)


