JEE Advance - Physics (2016 - Paper 2 Offline - No. 2)
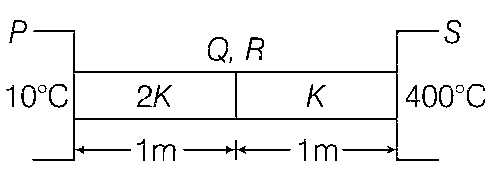
The ends Q and R of two thin wires, PQ and RS, are soldered (joined) together. Initially each of the wires
has a length of 1 m at 10oC. Now the end P is maintained at 10oC, while the end S is heated and
maintained at 400oC. The system is thermally insulated from its surroundings. If the thermal conductivity
of wire PQ is twice that of the wire RS and the coefficient of linear thermal expansion of PQ is 1.2 $$ \times $$ 10-5 K-1 , the change in length of the wire PQ is
0.78 mm
0.90 mm
1.56 mm
2.34 mm
Explanation
Rate of heat flow from P to Q,
$${{dQ} \over {dt}} = {{2KA(T - 10)} \over 1}$$
Rate of heat flow from Q to S,
$${{dQ} \over {dt}} = {{KA(4000 - T)} \over 1}$$
At steady state, state rate of heat flow is same
$$ \therefore $$ $${{2KA(T - 10)} \over 1} = KA(400 - T)$$
or $$2T - 20 = 400 - T$$ or $$3T = 420$$
$$ \therefore $$ $$T = 140^\circ $$
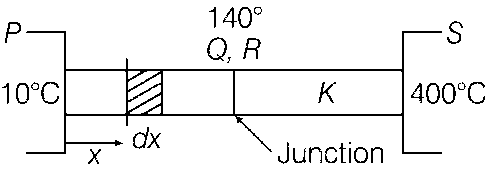
Temperature of junction is $$140^\circ $$C.
Temperature at a distance x from end P is $${T_x} = (130x + 10^\circ )$$
Change in length dx is suppose dy.
Then, $$dy = \alpha dx({T_x} - 10)$$
$$\int_0^{\Delta y} {dy} = \int_0^1 {\alpha dx(130x + 10 - 10)} $$
$$\Delta y = \left[ {{{\alpha {x^2}} \over 2} \times 130} \right]_0^1$$
$$\Delta y = 1.2 \times {10^{ - 5}} \times 65$$
$$\Delta y = 78.0 \times {10^{ - 5}}$$ m = 0.78 mm
Comments (0)


