Sign In

JEE Advance - Physics (2016 - Paper 2 Offline - No. 16)

A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $$\omega$$ is an example of a non-inertial frame of reference. The relationship between the force $$\overrightarrow F $$rot experienced by a particle of mass m moving on the rotating disc and the force $$\overrightarrow F $$in experienced by the particle in an inertial frame of reference is,

$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,

where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.

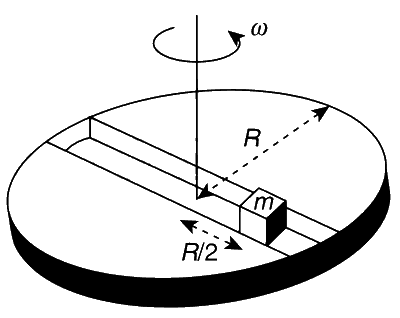
JEE Advanced 2016 Paper 2 Offline Physics - Rotational Motion Question 40 English
Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.

The net reaction of the disc on the block is
$$m{\omega ^2}R\sin \omega t\widehat j - mg\widehat k$$
$${1 \over 2}m{\omega ^2}R({e^{\omega t}} - {e^{ - \omega t}})\widehat j + mg\widehat k$$
$${1 \over 2}m{\omega ^2}R({e^{2\omega t}} - {e^{ - 2\omega t}})\widehat j + mg\widehat k$$
$$ - m{\omega ^2}R\cos \omega r\widehat j - mg\widehat k$$

Explanation

The rotational quantity of velocity given by

$${v_{rot}} = {{dr} \over {dt}} = {R \over 4}[\omega {e^{\omega t}} - \omega {e^{ - \omega t}}]$$

$${v_{rot}} = {{\omega R} \over 4}[{e^{\omega t}} - {e^{ - \omega t}}]$$ ...... (1)

The force experienced by the block in the inertial frame is

$${\overrightarrow F _{in}} = - m{\omega ^2}r\widehat i - mg\widehat k$$ ..... (2)

Therefore, the force experienced by the block in the rotating frame is

$${\overrightarrow F _{rot}} = {\overrightarrow F _{in}} + 2m({\overrightarrow v _{rot}} \times \omega \widehat k) + m(\omega \widehat k \times r\widehat i) \times \omega \widehat k$$

$${\overrightarrow F _{rot}} = ( - m{\omega ^2}r\widehat i - mg\widehat k) + 2m{{\omega R} \over r}[{e^{\omega t}} - {e^{ - \omega t}}]\widehat i \times \omega \widehat k + m{\omega ^2}r\widehat i$$

$$ = - {{m{\omega ^2}R} \over 2}[{e^{\omega t}} - {e^{ - \omega t}}]\widehat j - mg\widehat k$$

Therefore, the net reaction of the disc on the block is

$${\overrightarrow F _{reaction}} - {\overrightarrow F _{rot}} = {{m{\omega ^2}R} \over 2}[{e^{\omega t}} - {e^{\omega t}}]\widehat j + mg\widehat k$$

Hence, option (B) is correct.

Comments (0)

Advertisement