JEE Advance - Physics (2016 - Paper 2 Offline - No. 15)
$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,
where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.
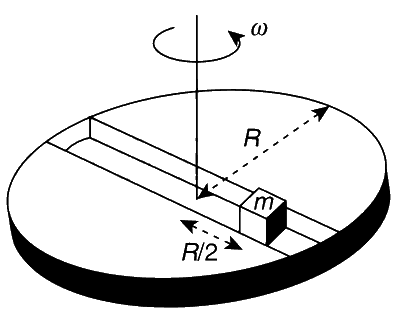
Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.
The distance r of the block at time t is
Explanation
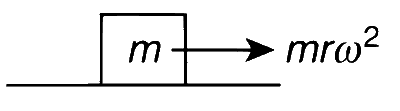
The given particle of mass m experiences a centrifugal force:
F = ma = mr$$\omega$$2
$$\Rightarrow$$ a = r$$\omega$$2
$$\Rightarrow$$ $${{dv} \over {dt}} = r{\omega ^2}$$
or, $$\left( {{{dv} \over {dr}}} \right)\left( {{{dr} \over {dt}}} \right) = r{\omega ^2}$$ ($$\because$$ $${{{dr} \over {dt}}}=v$$)
$$ \Rightarrow vdv = r{\omega ^2}dr$$
$$\int\limits_0^v {vdv = {\omega ^2}\int\limits_{R/2}^r {rdr} } $$ ($$\because$$ at t = 0, $$r = {R \over 2}$$)
$$ \Rightarrow {{{v^2}} \over 2} = {\omega ^2}\left( {{{{r^2}} \over 2}} \right)_{R/2}^r$$
$$ \Rightarrow v = \omega \sqrt {{r^2} - {{{R^2}} \over 4}} $$
Now, $$v = {{dr} \over {dt}}$$
Therefore, $${{dr} \over {dt}} = \omega \sqrt {{r^2} - {{{R^2}} \over 4}} $$
or, $$\int\limits_{R/2}^r {{{dr} \over {\sqrt {{r^2} - {{{R^2}} \over 4}} }} = \omega \int\limits_0^t {dt} } $$ ...... (1)
To solve this integral, we substitute $$r = {R \over 2}\sec \theta $$; therefore,
$$dr = {R \over 2}\sec \theta \tan \theta d\theta $$
$$ \Rightarrow \int\limits_{{\pi \over 2}}^{{{\sec }^{ - 1}}(2r/R)} {{{(r/2)\sec \theta \tan \theta d\theta } \over {\sqrt {{{{R^2}} \over 4}{{\tan }^2}\theta } }} = \omega t} $$
$$ \Rightarrow \omega t = \int\limits_{\pi /2}^{{{\sec }^{ - 1}}(2r/R)} {\sec \theta d\theta } $$
$$ = {\left[ {\ln \left| {\sec \theta + \tan \theta } \right|} \right]^{{{\sec }^{ - 1}}(2r/R)}}$$
$$ = \left[ {\ln \left| {\sec \theta + \sqrt {{{\sec }^2}\theta - 1} } \right|} \right]_{\pi /2}^{{{\sec }^{ - 1}}(2r/R)}$$
$$ \Rightarrow \omega t = \ln \left[ {{{2r} \over R} + {{\sqrt {4{r^2} - {R^2}} } \over R}} \right]$$
Let $${{2r} \over R} = x$$. Therefore,
$${e^\omega } = x + \sqrt {{x^2} - 1} $$
$$ \Rightarrow ({e^{\omega t}} - x)^2 = {x^2} - 1$$
$$ \Rightarrow {e^{2\omega t}} - 2x{e^{\omega t}} + x^2 = x^2 - 1$$
$$ \Rightarrow {e^{2\omega t}} - 2x{e^{\omega t}} + 1 = 0$$
$$ \Rightarrow x = {{{e^{2\omega t}} + 1} \over {2{e^{\omega t}}}} = {{{e^{\omega t}} + {e^{ - \omega t}}} \over 2}$$
On replacing x by $${{2r} \over R}$$, we get
$${{2r} \over R} = {{{e^{\omega t}} + {e^{ - \omega t}}} \over 2}$$
or, $$r = {R \over 4}[{e^{\omega t}} + {e^{ - \omega t}}]$$
Hence, option (c) is correct.
Comments (0)


