JEE Advance - Physics (2016 - Paper 2 Offline - No. 14)
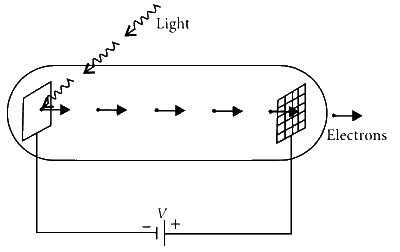
Explanation
In photo-electric effect, the maximum kinetic energy of the photo-electron ejected at the cathode, is given by
$${K_{\max ,\,c}} = {{hc} \over {{\lambda _{ph}}}} - \phi $$,
where $$\lambda$$ph is the wavelength of the incident light and $$\phi$$ is the work function of the material. The ejected photoelectrons are accelerated from the cathode to the anode by a potential V. Thus, the maximum kinetic energy of the photo-electron at the anode is
$${K_{\max ,\,a}} = {K_{\max ,\,c}} + eV = {{hc} \over {{\lambda _{ph}}}} - \phi + eV$$.
Now, minimum de-Broglie wavelength of electrons passing through anode,
$${\lambda _e} = {h \over {\sqrt {2m\,{K_{\max ,\,a}}} }} = {h \over {\sqrt {2m\left( {{{hc} \over {{\lambda _{ph}}}} - \phi + eV} \right)} }}$$ ...... (i)
D : For $$V > > \phi e$$
$${\lambda _e} \approx {h \over {\sqrt {2meV} }} \propto {1 \over {\sqrt V }}$$
$$\therefore$$ If V is made four times, $$\lambda$$e becomes $${1 \over {\sqrt 4 }} = {1 \over 2}$$, i.e. halved.
C : When $$\phi$$ and $$\lambda$$ph increases, $$\lambda$$e also increases.
A : From (i)
$${{d{\lambda _e}} \over {dt}} = {{ - h} \over 2}{\left[ {2m\left( {{{hc} \over {{\lambda _{ph}}}} - \phi + eV} \right)} \right]^{ - 3/2}} \times 2m\left( {{{ - hc} \over {\lambda _{ph}^2}}} \right){{d{\lambda _{ph}}} \over {dt}}$$
$$ \Rightarrow {{d{\lambda _e}} \over {dt}} \ne {{d{\lambda _{ph}}} \over {dt}}$$
I : $$\lambda$$e does not depend on d.
Comments (0)


