JEE Advance - Physics (2016 - Paper 2 Offline - No. 13)
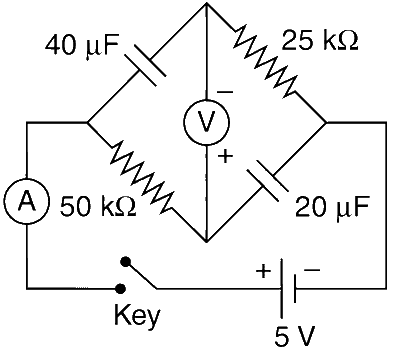
Explanation

When the key is just pressed, there is no charge on capacitors
$$\therefore$$ $$5 = 25000{I_1} \Rightarrow {I_1} = {5 \over {25000}} = 0.2\,mA$$
and $$5 = 50000{I_2} \Rightarrow {I_2} = {5 \over {50000}} = 0.1\,mA$$
Reading of voltmeter $$ = {V_Q} - {V_P} = - 25000{I_1}$$
$$ = - 25000 \times 0.2 \times {10^{ - 3}}V = - 5V$$
After a very long time, steady state is reached, i.e. $${I_1} - {I_2} = 0$$
$$\therefore$$ $$5 = {{{q_1}} \over {40 \times {{10}^{ - 6}}}}$$ or $${q_1} = 200\mu C$$
and $$\therefore$$ $$5 = {{{q_2}} \over {20 \times {{10}^{ - 6}}}}$$ or $${q_2} = 100\mu C$$
Now, reading of voltmeter $$ = {V_Q} - {V_P}$$
$$ = {{{q_2}} \over {20\mu F}} = {{100\mu C} \over {20\mu F}} = 5V$$
For capacitor of 40$$\mu$$F,
$${\tau _1} = RC = 25 \times {10^3} \times 40 \times {10^{ - 6}} = 1\,s$$
and for capacitor of 20$$\mu$$F,
$${\tau _2} = RC = 50 \times {10^3} \times 20 \times {10^{ - 6}} = 1\,s$$
$$\therefore$$ At any instant t,
$${q_1} = 200[1 - {e^{ - t}}]\mu C$$, $${q_2} = 100[1 - {e^{ - t}}]\mu C$$
$${I_1} = 0.2\,{e^{ - t}}$$ mA, $${I_2} = 0.1\,{e^{ - t}}$$ mA
$${V_Q} - {V_P} = {{100(1 - {e^{ - t}})\mu C} \over {20\mu F}} - 25k\Omega \times 0.2\,{e^{ - t}}$$ mA
$$ = 5(1 - {e^{ - t}}) - 5{e^{ - t}} = 5 - 10{e^{ - t}}$$
At t = ln 2 s; $${V_Q} - {V_P} = 5 - 10{e^{ - \ln 2}} = 5 - {{10} \over 2} = 0$$ V
Initially, I0 = 0.1 mA + 0.2 mA = 0.3 mA
At t = 1 s, I = I1 + I2
$$ = (0.2{e^{ - 1}} + 0.1{e^{ - 1}}) = {{0.3} \over e}\,mA = {{{I_0}} \over e}$$
After a long time, i.e. t $$\to$$ $$\infty$$
$$I = {I_1} + {I_2} = 0.2{e^{ - \infty }} + 0.1{e^{ - \infty }} = 0$$
Comments (0)


