JEE Advance - Physics (2016 - Paper 2 Offline - No. 11)
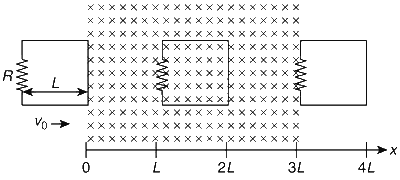
Which of the following schematic plot(s) is (are) correct? (Ignore gravity)
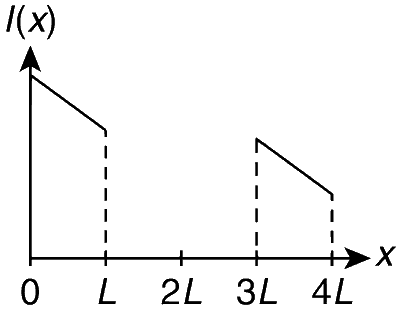
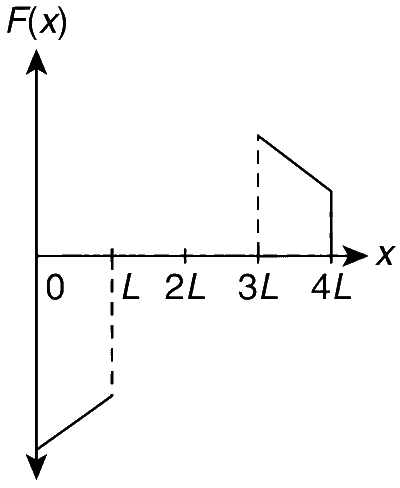
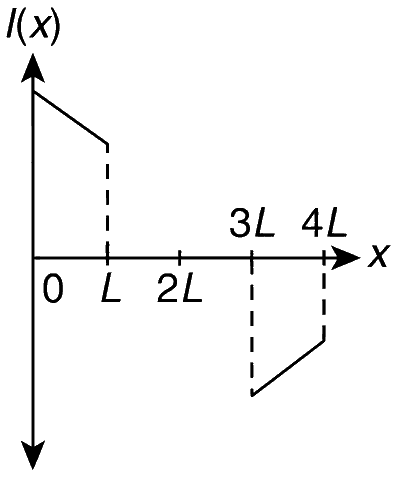

Explanation
We discuss the following cases :
$$\bullet$$ For x = 0 $$\to$$ L : The induced emf in the loop is
$$\varepsilon = v{B_0}L$$
Therefore, the induced current is
$$I = {{v{B_0}L} \over R}$$ ........ (1)
As the flux is increasing, the current passes in counterclockwise direction and oppose the existing magnetic field (i.e., Lenz's law).
Let us consider the loop which is labelled as shown in the following figure:
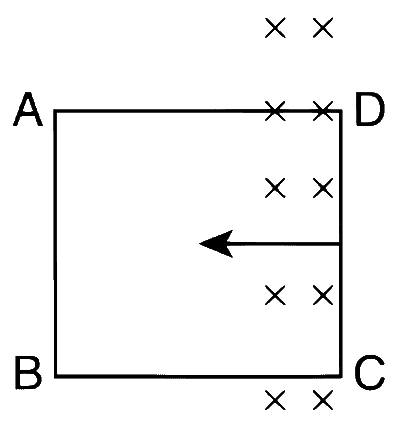
Force on the side CD of the loop is
$$\overrightarrow F = i(\overrightarrow L \times \overrightarrow B ) = {{v{B_0}L} \over R}[L\widehat j \times {B_0}( - \widehat k)]$$
$$\overrightarrow F = - {{vB_0^2{L^2}} \over R}\widehat i$$ (towards left) ........ (2)
$$ \Rightarrow {{mdv} \over {dt}} = - {{B_0^2{L^2}} \over R}v$$
$$ \Rightarrow {{mdv} \over {dx}}.{{dx} \over {dt}} = - {{ - B_0^2{L^2}} \over R}v$$
$$ \Rightarrow \int\limits_{{v_0}}^v {dv = - {{B_0^2{L^2}} \over {mR}}\int\limits_0^x {dx} } $$ (Since $${{dx} \over {dt}} = v$$)
$$ \Rightarrow v = {v_0} - {{B_0^2{L^2}} \over {mR}}x$$ ....... (3)
From Eqs. (1) and (3), we get
$$I = {{{v_0}{B_0}L} \over R} - {{B_0^3{L^3}} \over {m{R^2}}}x$$ ....... (4)
From Eqs. (2) and (3), we get
$$\overrightarrow F = - {{{v_0}B_0^2{L^2}} \over R} + {{B_0^4{L^4}} \over {m{R^2}}}x$$
$$\bullet$$ For x = L $$\to$$ 3L: Here, there is no change in flux and hence there is no induced current and thereby there is no force and no change in velocity.
$$\bullet$$ For x = 3L $$\to$$ 4L :
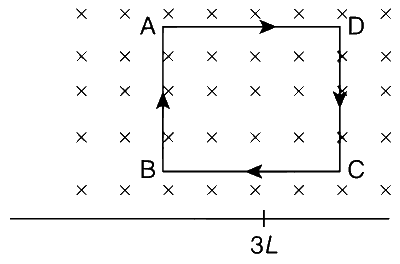
As the flux is decreasing, the current passes in clockwise direction and supports the existing magnetic field (i.e., Lenz's law).
Hence, option (A) is incorrect.
Consequently, the magnetic force experienced by the arm AB of the loop is
$$\overrightarrow F = i(\overrightarrow L \times \overrightarrow B ) = {{v{B_0}L} \over R}[L\widehat j \times {B_0}( - \widehat k)]$$
$$ = - {{vB_0^2{L^2}} \over R}\widehat i$$ (towards left)
Hence, option (B) is incorrect.
Similarly, now we have
$$\int\limits_{{v_{3L}}}^v {dv = - {{B_0^2{L^2}} \over {mR}}\int\limits_{3L}^x {dx \Rightarrow v = {v_{3L}} - {{B_0^2{L^2}} \over {mR}}\left( {x - 3L} \right)} } $$
When the loop is completely within the magnetic field, the force and current is zero and velocity is constant. However, while coming out, the current passes in clockwise direction, the force exists in backwards and the velocity decreases linearly.
Comments (0)


