Let i_g be the current that gives full deflection of the galvanometer. When all components are connected in series (see figure), effective resistance of the circuit is $${R_e} = 2R + 2{R_c}$$ and maximum current allowed in the circuit is i_g.

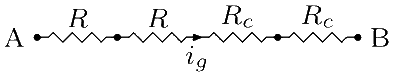
Thus, the voltage between A and B is

$${V_{AB}} = {i_g}{R_e} = 2{i_g}(R + {R_c})$$.

Consider the case when two resistors and one galvanometer are connected in series and the second galvanometer is connected in parallel.

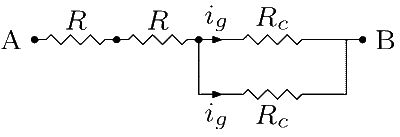
The maximum current through each galvanometer is i_g and the maximum current through the resistors is 2i_g. Apply Kirchhoff's law to get the voltage between A and B as

$$V{'_{AB}} = 2{i_g}R + 2{i_g}R + {i_g}{R_c}$$

$$ = 2{i_g}(R + {R_c}) + 2{i_g}(R - {R_c}/2)$$

$$ = {V_{AB}} + 2{i_g}(R - {R_c}/2)$$

$$ > {V_{AB}}$$ ($$\because$$ $${R_c} < R/2$$).

Consider the case when all four components are connected in parallel.

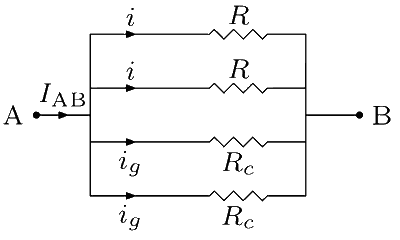
Let i and i_g be the currents through the resistors and the galvanometers. By Kirchhoff's law, $$iR = {i_g}{R_c}$$, which gives $$i = {i_g}{R_c}/R$$. The current between A and B is

$${I_{AB}} = 2i + 2{i_g} = 2{i_g}(1 + {R_c}/R)$$.

Consider the case when the two galvanometers are connected in series and the combination is connected in parallel with both the resistors.

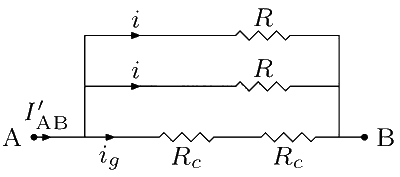
$$I{'_{AB}} = {i_g} + 2i = {i_g} + 2{i_g}(2{R_c}/R)$$

$$ = 2{i_g}(1 + {R_c}/R) - (1 - 2{R_c}/R){i_g}$$

$$ = {I_{AB}} - (1 - 2{R_c}/R){i_g}$$

$$ < {I_{AB}}$$ ($$\because$$ $${R_c} < R/2$$).