JEE Advance - Physics (2016 - Paper 1 Offline - No. 9)
A plano-convex lens is made of material of refractive index n. When a small object is placed 30 cm away in front of the curved surface of the lens, an image of double the size of the object is produced. Due to reflection from the convex surface of the lens, another faint image is observed at a distance of 10 cm away form the lens. Which of the following statement(s) is(are) true?
The refractive index of the lens is 2.5
The radius of curvature of the convex surface is 45 cm
The faint image is erect and real
The focal length of the lens is 20 cm
Explanation
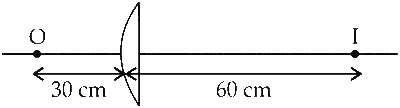
For refraction through plano - Convex lens,
$$ m=-2=\frac{v}{u} $$
$$ \begin{array}{ll} \Rightarrow v=-2 u \\\\ \text { As, } u=-30 \mathrm{~cm} \\\\ \Rightarrow v=60 \mathrm{~cm} \end{array} $$
Using lens formula, $\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$
$$ \begin{aligned} \frac{1}{60}-\frac{1}{-30} & =\frac{1}{f} \\\\ \Rightarrow f =20 \mathrm{~cm} \end{aligned} $$
By lens maker's formula,
$$ \begin{aligned} \frac{1}{f} & =(n-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right) \\\\ \Rightarrow \frac{1}{20} & =(n-1)\left(\frac{1}{\mathrm{R}}+\frac{1}{\infty}\right)=\frac{n-1}{\mathrm{R}} \\\\ \Rightarrow n & =1+\left(\frac{\mathrm{R}}{20}\right) ........(i) \end{aligned} $$
for poor reflection from convex surface,
$$ \begin{aligned} & u=-30 \mathrm{~cm}, \\\\ & v=10 \mathrm{~cm}, f=\mathrm{R} / 2 \end{aligned} $$
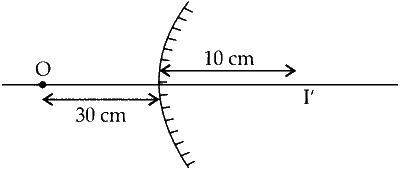
Using mirror formula,
$$ \begin{aligned} \frac{1}{v}+\frac{1}{u} & =\frac{1}{f}=\frac{2}{\mathrm{R}} ; \\\\ \Rightarrow \frac{1}{10}+\frac{1}{-30} & =\frac{2}{\mathrm{R}} \end{aligned} $$
$$ \begin{array}{llrl} \Rightarrow \frac{2}{\mathrm{R}} =\frac{2}{30} \\\\ \therefore \mathrm{R} =30 \mathrm{~cm} \end{array} $$
Substitute $R=30 \mathrm{~cm}$ in equation (i) to get $n=$ 2.5 for $f=20 \mathrm{~cm}$ (inverted image) and $n=1.5$ for $f=60 \mathrm{~cm}$ (erect image).
$$ m=-2=\frac{v}{u} $$
$$ \begin{array}{ll} \Rightarrow v=-2 u \\\\ \text { As, } u=-30 \mathrm{~cm} \\\\ \Rightarrow v=60 \mathrm{~cm} \end{array} $$
Using lens formula, $\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$
$$ \begin{aligned} \frac{1}{60}-\frac{1}{-30} & =\frac{1}{f} \\\\ \Rightarrow f =20 \mathrm{~cm} \end{aligned} $$

By lens maker's formula,
$$ \begin{aligned} \frac{1}{f} & =(n-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right) \\\\ \Rightarrow \frac{1}{20} & =(n-1)\left(\frac{1}{\mathrm{R}}+\frac{1}{\infty}\right)=\frac{n-1}{\mathrm{R}} \\\\ \Rightarrow n & =1+\left(\frac{\mathrm{R}}{20}\right) ........(i) \end{aligned} $$
for poor reflection from convex surface,
$$ \begin{aligned} & u=-30 \mathrm{~cm}, \\\\ & v=10 \mathrm{~cm}, f=\mathrm{R} / 2 \end{aligned} $$

Using mirror formula,
$$ \begin{aligned} \frac{1}{v}+\frac{1}{u} & =\frac{1}{f}=\frac{2}{\mathrm{R}} ; \\\\ \Rightarrow \frac{1}{10}+\frac{1}{-30} & =\frac{2}{\mathrm{R}} \end{aligned} $$
$$ \begin{array}{llrl} \Rightarrow \frac{2}{\mathrm{R}} =\frac{2}{30} \\\\ \therefore \mathrm{R} =30 \mathrm{~cm} \end{array} $$
Substitute $R=30 \mathrm{~cm}$ in equation (i) to get $n=$ 2.5 for $f=20 \mathrm{~cm}$ (inverted image) and $n=1.5$ for $f=60 \mathrm{~cm}$ (erect image).
Comments (0)


