JEE Advance - Physics (2016 - Paper 1 Offline - No. 6)
A parallel beam of light is incident from air at an anglea on the side PQ of a right angled triangular prism of refractive index n = $$\sqrt 2 $$. Light undergoes total internal reflection in the prism at the face PR when a has a minimum value of 45°. The angle q of the prism is :
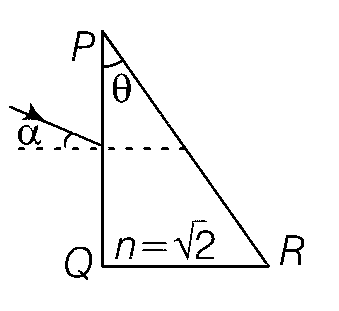
15o
22.5o
30o
45o
Explanation
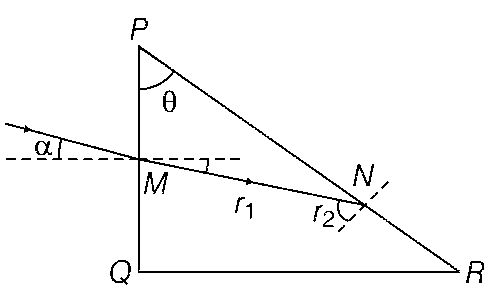 Applying Snell's law at M,
Applying Snell's law at M,$$n = {{\sin \alpha } \over {\sin {r_1}}} \Rightarrow \sqrt 2 = {{\sin 45^\circ } \over {\sin {r_1}}}$$
$$ \Rightarrow \sin {r_1} = {{\sin 45^\circ } \over {\sqrt 2 }} = {{1/\sqrt 2 } \over {\sqrt 2 }} = {1 \over 2}$$
$${r_1} = 30^\circ $$
$$\sin {\theta _c} = {1 \over n} = {1 \over {\sqrt 2 }} \Rightarrow {\theta _c} = 45^\circ $$
Let us take $${r_2} = {\theta _c} = 45^\circ $$ for just satisfying the condition of TIR.
In $$\Delta PNM$$,
$$\theta + 90 + {r_1} + 90 - {r_2} = 180^\circ $$
or $$\theta = {r_2} - {r_1} = 45^\circ - 30^\circ = 15^\circ $$
Note If $$\alpha$$ = 45$$^\circ $$ (the given value). Then, r1 > 30$$^\circ $$ (the obtained value)
$${r_2} > {\theta _c}$$ (as r2 $$-$$ r1 = $$\theta$$ or r2 = $$\theta$$ + r1)
or TIR will take place. So, for taking TIR under all conditions $$\alpha$$ should be greater than 45$$^\circ$$ or this is the minimum value of $$\alpha$$.
Comments (0)


