JEE Advance - Physics (2016 - Paper 1 Offline - No. 5)
A uniform wooden stick of mass 1.6 kg and length $$l$$ rests in an inclined manner on a smooth, vertical wall
of height h ( < $$l$$ ) such that a small portion of the stick extends beyond the wall. The reaction force of the
wall on the stick is perpendicular to the stick. The stick makes an angle of $$30^\circ $$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio $${h \over l}$$ and the frictional force f at the bottom of the stick are ( g =10 ms-2 )
$${h \over l} = {{\sqrt 3 } \over {16}},f = {{16\sqrt 3 } \over 3}N$$
$${h \over l} = {3 \over {16}},f = {{16\sqrt 3 } \over 3}N$$
$${h \over l} = {{3\sqrt 3 } \over {16}},f = {{8\sqrt 3 } \over 3}N$$
$${h \over l} = {{3\sqrt 3 } \over {16}},f = {{16\sqrt 3 } \over 3}N$$
Explanation
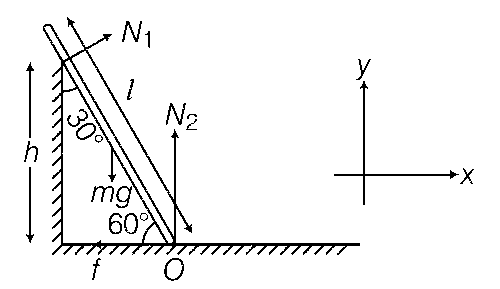
$$\sum {{F_x} = 0} $$, $${N_1}\cos 30^\circ - f = 0$$ .... (i)
$$\sum {{F_y} = 0} $$, $${N_1}\sin 30^\circ + {N_2} - mg = 0$$ .... (ii)
$$\sum {{\tau _0} = 0} $$
$$mg{1 \over 2}\cos 60^\circ - {N_1}{h \over {\cos 30^\circ }} = 0$$ .... (iii)
Also, given $${N_1} = {N_2}$$ .... (iv)
Solving Eqs. (i), (ii), (iii) and (iv) we have
$${h \over l} = {{3\sqrt 3 } \over {16}}$$ and $$f = {{16\sqrt 3 } \over 3}$$
Comments (0)


