Let the charge per unit length on the axis be $$\lambda$$(t) at a time t. The electric field due to this line charge at a radial distance r is given by

$$\overrightarrow E (r,t) = {{\lambda (t)} \over {2\pi \in r}}\widehat r$$. ...... (1)

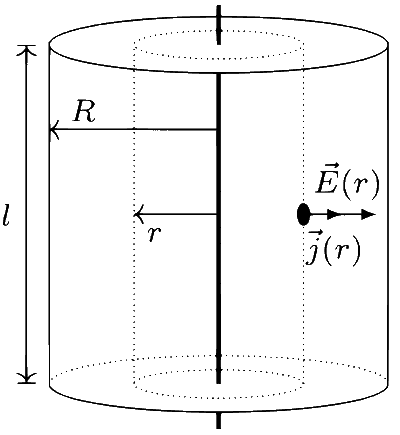
The free charges inside the conductor start moving radially due to the presence of electric field. The current density at a point is defined as the current flowing across a unit area placed perpendicular to the direction of current flow. The current density at a point is related to the electric field at that point by Ohm's law i.e.,

$$\overrightarrow j (r,t) = \sigma \overrightarrow E (r,t)$$, ....... (2)

where $$\sigma$$ is the electrical conductivity of the conductor. The current through a cylindrical shell of radius r and length l is given by

$$I = \int_{surface} {\overrightarrow j (r,t)\,.\,d\overrightarrow A = j(r,t)(2\pi rl)} $$. ...... (3)

By conservation of charge, the current I is equal to the rate of decrease of charge q on axial line segment of length l i.e.,

$$I = - {{dq} \over {dt}} = - l{{d\lambda (t)} \over {dt}}$$. ...... (4)

From equations (1) - (4)

$${{d\lambda (t)} \over {dt}} = - {{\sigma \lambda (t)} \over \in }$$.

Integrate with initial condition $$\lambda$$(t = 0) = $$\lambda$$₀ to get

$$\lambda (t) = {\lambda _0}\exp {e^{ - {{\sigma t} \over \in }}}$$,

Substitute $$\lambda$$(t) in equation (2) to get

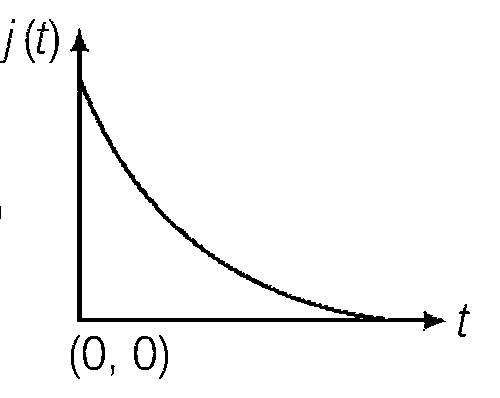
$$\overrightarrow j (r,t) = {{\sigma {\lambda _0}} \over {2\pi \in r}}{e^{ - {{\sigma t} \over \in }}}$$.

Note that current density varies as 1/r with radial distance r. It decreases exponentially with time and becomes zero at t $$\to$$ $$\infty$$.