JEE Advance - Physics (2016 - Paper 1 Offline - No. 15)
A hydrogen atom in its ground state is irradiated by light of wavelength 970$$\mathop A\limits^o $$.
Taking hc = 1.237 $$\times$$ 10$$-$$6 eVm and the ground state energy of hydrogen atom as $$-$$ 13.6 eV, the number of lines present in the emission spectrum is
Taking hc = 1.237 $$\times$$ 10$$-$$6 eVm and the ground state energy of hydrogen atom as $$-$$ 13.6 eV, the number of lines present in the emission spectrum is
Answer
6
Explanation
The energy of the incident photon of wavelength $\lambda=970 $ $$\mathop A\limits^o $$ is
$$ \Delta E=\frac{h c}{\lambda}=\frac{1.237 \times 10^{-6}}{970 \times 10^{-10}}=12.75 \mathrm{eV} $$
$$ \begin{aligned} & \text { Final energy of electron in } n^{\text {th }} \text { state }=-\frac{13.6}{n^2} \mathrm{eV} \\\\ & \Rightarrow-\frac{13.6}{n^2}=-13.6+12.75=-0.85 \\\\ & \Rightarrow n^2=16 \Rightarrow n=4 \end{aligned} $$
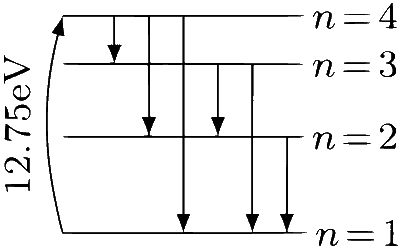
The hydrogen atom can make ${ }^n \mathrm{C}_2=6$ transitions while returning to ground state. Thus, the emission spectrum will have six lines.
$$ \Delta E=\frac{h c}{\lambda}=\frac{1.237 \times 10^{-6}}{970 \times 10^{-10}}=12.75 \mathrm{eV} $$
$$ \begin{aligned} & \text { Final energy of electron in } n^{\text {th }} \text { state }=-\frac{13.6}{n^2} \mathrm{eV} \\\\ & \Rightarrow-\frac{13.6}{n^2}=-13.6+12.75=-0.85 \\\\ & \Rightarrow n^2=16 \Rightarrow n=4 \end{aligned} $$

The hydrogen atom can make ${ }^n \mathrm{C}_2=6$ transitions while returning to ground state. Thus, the emission spectrum will have six lines.
Comments (0)


