JEE Advance - Physics (2016 - Paper 1 Offline - No. 12)
A transparent slab of thickness d has a refractive index n (z) that increases with z. Here, z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2 (> n1), as shown in the figure. A ray of light is incident with angle $$\theta$$i from medium 1 and emerges in medium 2 with refraction angle $$\theta$$f with a lateral displacement $l$.

Which of the following statement(s) is (are) true?

Which of the following statement(s) is (are) true?
$l$ is dependent on n(z)
n1 sin$$\theta$$i = (n2 $$-$$ n1) sin$$\theta$$f
n1 sin$$\theta$$i = n2 sin$$\theta$$f
$l$ is independent of n2
Explanation
From Snell's law,
$$ \begin{aligned} n_1 \sin \theta_i=n\left(z_1\right) \sin \theta_{z_1}=n\left(z_2\right) \sin \theta_{z_2} & =\ldots \ldots \\\\ \ldots & =n(d) \sin \theta_d=n_2 \sin \theta_f \end{aligned} $$
The lateral displacement of a ray by a parallel slab depends on the angle of incidence $\theta_i$, refractive index $n_1$, slab thickness $d$ and the refractive index of the slab $n$ (it is independent of $n_2$ because $l$ is measured before the start of medium 2, there is no effect of $n_2$ on $l$ ). Consider the parallel slab shown in the figure.
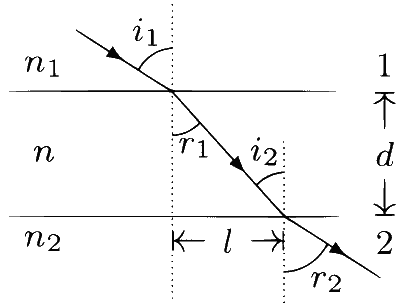
By Snell's law, $n_1 \sin i_1=n \sin r_1$ and $n \sin i_2=$ $n_2 \sin r_2$. By geometry, $i_2=r_1$ and the lateral displacement is given by
$$ l=d \frac{\sin r_1}{\cos r_1}=\frac{d n_1 \sin i_1}{\sqrt{n^2-n_1^2 \sin ^2 i_1}} . $$
Hence, $l$ is independent of $n_2$ but it is dependent of $n(z)$.
$$ \begin{aligned} n_1 \sin \theta_i=n\left(z_1\right) \sin \theta_{z_1}=n\left(z_2\right) \sin \theta_{z_2} & =\ldots \ldots \\\\ \ldots & =n(d) \sin \theta_d=n_2 \sin \theta_f \end{aligned} $$
The lateral displacement of a ray by a parallel slab depends on the angle of incidence $\theta_i$, refractive index $n_1$, slab thickness $d$ and the refractive index of the slab $n$ (it is independent of $n_2$ because $l$ is measured before the start of medium 2, there is no effect of $n_2$ on $l$ ). Consider the parallel slab shown in the figure.

By Snell's law, $n_1 \sin i_1=n \sin r_1$ and $n \sin i_2=$ $n_2 \sin r_2$. By geometry, $i_2=r_1$ and the lateral displacement is given by
$$ l=d \frac{\sin r_1}{\cos r_1}=\frac{d n_1 \sin i_1}{\sqrt{n^2-n_1^2 \sin ^2 i_1}} . $$
Hence, $l$ is independent of $n_2$ but it is dependent of $n(z)$.
Comments (0)


