JEE Advance - Physics (2016 - Paper 1 Offline - No. 11)
Two loudspeakers M and N are located 20m apart and emit sound at frequencies 118 Hz and 121 Hz, respectively. A car in initially at a point P, 1800 m away from the midpoint Q of the line MN and moves towards Q constantly at 60 km/h along the perpendicular bisector of MN. It crosses Q and eventually reaches a point R, 1800 m away from Q.
Let v(t) represent the beat frequency measured by a person sitting in the car at time t. Let vP, vQ and vR be the beat frequencies measured at locations P, Q and R respectively. The speed of sound in air is 330 ms$$-$$1. Which of the following statement(s) is (are) true regarding the sound heard by the person?
Let v(t) represent the beat frequency measured by a person sitting in the car at time t. Let vP, vQ and vR be the beat frequencies measured at locations P, Q and R respectively. The speed of sound in air is 330 ms$$-$$1. Which of the following statement(s) is (are) true regarding the sound heard by the person?
The plot below represents schematically the variation of beat frequency with time
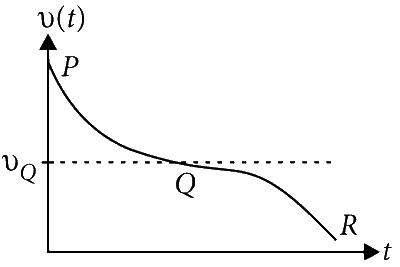

The rate of change in beat frequency is maximum when the car passes through Q
vP + vR = 2vQ
The plot below represents schematically the variations of beat frequency with time
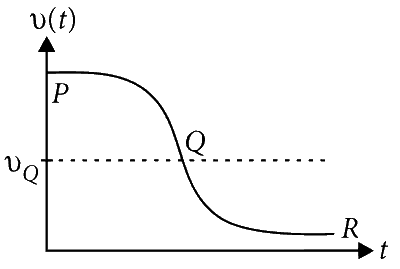

Explanation
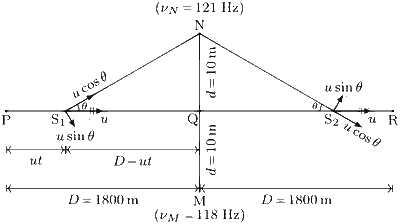
Consider the time $t\left(\leq t_Q\right)$ when car is at $S_1$ between $P$ and $Q$. The distance travelled by the car in time $t$ is $\mathrm{PS}_1=u t$. At this instant, the lines $\mathrm{S}_1{N}$ and $\mathrm{S}_1 \mathrm{M}$ both make angle $\theta$ with the velocity vector $\vec{u}$. The component of observer (person sitting in the car) velocity towards the sources $N$ and $M$ is $u_o=u \cos \theta$. The sources $N$ and $M$ are at rest i.e., $u_s=0$. Apply Doppler's effect equation to get frequencies of the sources $N$ and $M$ heard by the observer as
$$ \begin{aligned} \nu_N^{\prime} & =\frac{v+u_o}{v-u_s} \nu_N=\frac{v+u \cos \theta}{v} \nu_N \\\\ & =\left(1+\frac{u}{v} \frac{D-u t}{\sqrt{d^2+(D-u t)^2}}\right) \nu_N, \\\\ \nu_M^{\prime} & =\frac{v+u_o}{v-u_s} \nu_M=\frac{v+u \cos \theta}{v} \nu_M \\\\ & =\left(1+\frac{u}{v} \frac{D-u t}{\sqrt{d^2+(D-u t)^2}}\right) \nu_M . \end{aligned} $$
The beat frequency heard by the observer at time $t(\leq$ $\left.t_Q\right)$ is
$$ \begin{aligned} \nu(t) & =\nu_N^{\prime}-\nu_M^{\prime} \\\\ & =\left(1+\frac{u}{v} \frac{D-u t}{\sqrt{d^2+(D-u t)^2}}\right)\left(\nu_N-\nu_M\right) ........(1) \end{aligned} $$
Now, consider the time $t\left(\geq t_Q\right)$ when car is at $S_2$ between $Q$ and $R$. The distance travelled by the car in time $t$ is $\mathrm{PS}_2=u t$. At this instant, the lines $\mathrm{S}_2 \mathrm{~N}$ and $\mathrm{S}_2 \mathrm{M}$ both make angle $\left(180^{\circ}-\theta\right)$ with the velocity vector $\vec{u}$. The component of observer velocity towards the sources $N$ and $M$ is $u_o=-u \cos \theta$. Apply Doppler's effect equation to get
$$ \begin{aligned} \nu_N^{\prime} & =\frac{v+u_o}{v-u_s} \nu_N=\frac{v-u \cos \theta}{v} \nu_N \\\\ & =\left(1-\frac{u}{v} \frac{u t-D}{\sqrt{d^2+(u t-D)^2}}\right) \nu_N, \\\\ \nu_M^{\prime} & =\frac{v+u_o}{v-u_s} \nu_M=\frac{v-u \cos \theta}{v} \nu_M \\\\ & =\left(1-\frac{u}{v} \frac{u t-D}{\sqrt{d^2+(u t-D)^2}}\right) \nu_M . \end{aligned} $$
The beat frequency heard by the observer at time $t(\geq$ $\left.t_Q\right)$ is
$$ \begin{aligned} \nu(t) & =\nu_N^{\prime}-\nu_M^{\prime} \\\\ & =\left(1-\frac{u}{v} \frac{u t-D}{\sqrt{d^2+(u t-D)^2}}\right)\left(\nu_N-\nu_M\right) ..........(2) \end{aligned} $$
Substitute $t=0$ and $t=t_Q={D \over u}$ in equation (1) to get $\nu_P$ and $\nu_Q$ and substitute $t=t_R=2 {D \over u}$ in equation (2) to get $\nu_R$ i.e.,
$$ \begin{aligned} & \nu_P=\nu(t=0)=\left(1+\frac{u}{v} \frac{D}{\sqrt{d^2+D^2}}\right)\left(\nu_N-\nu_M\right) \\\\ & \nu_Q=\nu(t=D / u)=\left(\nu_N-\nu_M\right) \\\\ & \nu_R=\nu(t=2 D / u)=\left(1-\frac{u}{v} \frac{D}{\sqrt{d^2+D^2}}\right)\left(\nu_N-\nu_M\right) \end{aligned} $$
$$ \therefore $$ $$ \nu_P+\nu_R=2 \nu_Q $$
Differentiate equations (1) w.r.t. time t to get rate of change of beat frequency
$$ \frac{\mathrm{d} \nu(t)}{\mathrm{d} t}=-\left(\nu_N-\nu_M\right) \frac{u^2}{v} \frac{d^2}{\left(d^2+(D-u t)^2\right)^{3 / 2}} $$ ...........(3)
From equation (3), the slope is negative and its magnitude is maximum when $t={D \over u}=t_Q$ (denominator is minimum). Thus the rate of change of beat frequency is maximum when car passes through $Q$.
Comments (0)


