JEE Advance - Physics (2016 - Paper 1 Offline - No. 10)
A conducting loop in the shape of a right angled isosceles triangle of height 10 cm is kept such that the 90$$^\circ$$ vertex is very close to an infinitely long conducting wire (see the figure). The wire is electrically insulated from the loop. The hypotenuse of the triangle is parallel to the wire. The current in the triangular loop is in counterclockwise direction and increased at a constant rate of 10 As$$-$$1. Which of the following statement(s) is (are) true?


There is a repulsive force between the wire and the loop.
If the loop is rotated at a constant angular speed about the wire, an additional emf of $$\left( {{{{\mu _0}} \over \pi }} \right)$$ volt is induced in the wire
The magnitude of induced emf in the wire is $$\left( {{{{\mu _0}} \over \pi }} \right)$$ volt
The induced current in the wire is in opposite direction to the current along the hypotenuse.
Explanation
The flux passing through the triangular wire if ' $i$ ' current flows through the infinitely long conducting wire.
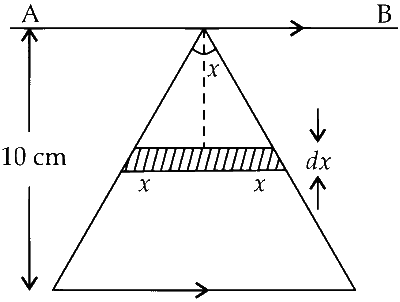
$$ \begin{aligned} \frac{d \mathrm{I}}{d t} & =10 \mathrm{As}^{-1} \\\\ \phi & =\int_0^{0.1} \frac{\mu_0 i}{2 \pi x} \times 2 x d x \\\\ \phi & =\frac{\mu_0 i}{10 \pi}=\mathrm{M} i \end{aligned} $$
$$ \therefore \mathrm{M}=\frac{\mu_0}{10 \pi} $$
$$ \text { Induced emf in the wire }=\frac{\mathrm{M} d i}{d t}=\frac{\mu_0}{10 \pi} \times 10=\frac{\mu_0}{\pi} $$
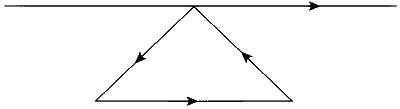
According to Lenz's law, the induced current opposes the flux change that creates it. Since the flux is increasing, the induced emf opposes the existing magnetic field and the current flows from left to right in the straight wire, that is, along the hypotenuse current. That is, there is a repulsive force between the wire and the loop.
Also, if the loop is rotated about the wire, there is no change in the flux through the wire, so no extra induced emf is generated in the wire.

$$ \begin{aligned} \frac{d \mathrm{I}}{d t} & =10 \mathrm{As}^{-1} \\\\ \phi & =\int_0^{0.1} \frac{\mu_0 i}{2 \pi x} \times 2 x d x \\\\ \phi & =\frac{\mu_0 i}{10 \pi}=\mathrm{M} i \end{aligned} $$
$$ \therefore \mathrm{M}=\frac{\mu_0}{10 \pi} $$
$$ \text { Induced emf in the wire }=\frac{\mathrm{M} d i}{d t}=\frac{\mu_0}{10 \pi} \times 10=\frac{\mu_0}{\pi} $$
According to Lenz's law, the induced current opposes the flux change that creates it. Since the flux is increasing, the induced emf opposes the existing magnetic field and the current flows from left to right in the straight wire, that is, along the hypotenuse current. That is, there is a repulsive force between the wire and the loop.

Also, if the loop is rotated about the wire, there is no change in the flux through the wire, so no extra induced emf is generated in the wire.
Comments (0)


