JEE Advance - Physics (2015 - Paper 2 Offline - No. 3)
The densities of two solid spheres A and B of the same radii R vary with radial distance r as $${\rho _A}(r) = k\left( {{r \over R}} \right)$$ and $${\rho _B}(r) = k{\left( {{r \over R}} \right)^5}$$, , respectively, where k is a constant. The moments of inertia of the individual spheres about axes passing through their centres are $${I_A}$$ and $${I_B}$$, respectively. If, $${{{I_B}} \over {{I_A}}} = {n \over {10}}$$, the value of n is
Answer
6
Explanation
Consider a spherical shell of radius r and small thickness dr.
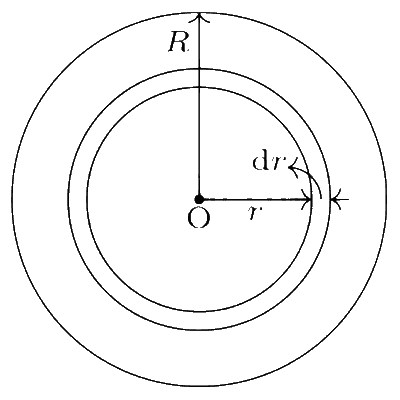
The volume of the shell is $$dV = 4\pi {r^2}dr$$ and its mass is
$$dm = \rho dV = 4\pi \rho {r^2}dr$$.
The moment of inertia of the spherical shell of mass dm and radius r about an axis passing through its centre O is given by $$dI = {2 \over 3}dm\,{r^2}$$. Substitute the expressions for dm and $$\rho$$ and then integrate to get the moment of inertia of the two spheres.
$${I_A} = \int_0^R {{2 \over 3}(4\pi {\rho _A}{r^4})dr = {{8\pi k} \over {3R}}\int_0^R {{r^5}dr = {{8\pi k{R^5}} \over {18}}} } $$,
$${I_B} = \int_0^R {{2 \over 3}(4\pi {\rho _B}{r^4})dr = {{8\pi k} \over {3{R^5}}}\int_0^R {{r^9}dr = {{8\pi k{R^5}} \over {30}}} } $$.
Divide to get $${I_B}/{I_A} = 6/10$$.
Comments (0)


