Sign In

JEE Advance - Physics (2015 - Paper 2 Offline - No. 18)

Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
If two structures of same cross-sectional area, but different numeral apertures NA1 and NA2 (NA2 < NA1) are joined longitudinally, the numerical aperture of the combined structure is
$${{N{A_1}N{A_2}} \over {N{A_1} + N{A_2}}}$$
$$N{A_1} + N{A_2}$$
$$N{A_1}$$
$$N{A_2}$$

Explanation

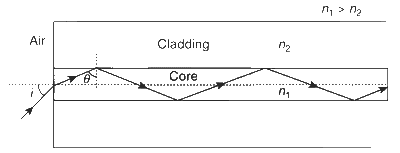
$$ \sin i_m=n_1 \sin \left(90-\theta_c\right) $$

$$ \Rightarrow \sin i_m=n_1 \cos \theta_c $$

$$ \begin{aligned} \Rightarrow N A & =n_1 \sqrt{1-\sin ^2 \theta_c} \\\\ & =n_1 \sqrt{1-\frac{n_2^2}{n_1^2}}=\sqrt{n_1^2-n_2^2} \end{aligned} $$

Substituting the values we get,

$$ N A_1=\frac{3}{4} $$

$$ \text { and } N A_2=\frac{\sqrt{15}}{5}=\sqrt{\frac{3}{4}} $$

and $$ N A_2 < N A_1 $$

Therefore, the numerical aperture of combined structure is equal to the lesser of the two numerical aperture, which is $N A_2$.

Comments (0)

Advertisement