Sign In

JEE Advance - Physics (2015 - Paper 2 Offline - No. 17)

Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
For two structures namely S1 with n1 = $${{\sqrt {45} } \over 4}$$ and n2 = $${3 \over 2}$$, and S2 with n1 = $${8 \over 5}$$ and n2 = $${7 \over 5}$$ and taking the refractive index of water to be $${4 \over 3}$$ and that to air to be 1, the correct options is/are :
NA of S1 immersed in water is the same as that of S2 immersed in a liquid of refractive index $${{16} \over {3\sqrt {15} }}$$
NA of S1 immersed in liquid of refractive index $${6 \over {\sqrt {15} }}$$ is the same as that of S2 immersed in water
NA of S1 placed in air is the same as that S2 immersed in liquid of refractive index $${4 \over {\sqrt {15} }}$$
NA of S1 placed in air is the same as that of S2 placed in water

Explanation

Let the whole structure be placed in the medium of refractive index n0. From geometry, if the angle of incidence at Q is $$\theta$$ then the angle of refraction at P is 90$$^\circ$$ $$-$$ $$\theta$$.

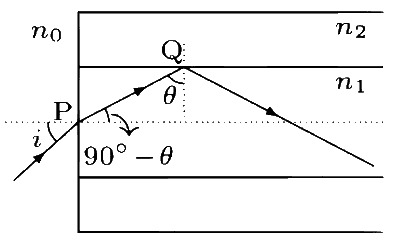
JEE Advanced 2015 Paper 2 Offline Physics - Geometrical Optics Question 40 English Explanation

The ray will undergo total internal reflection at Q if the angle of incidence at Q is greater than or equal to the critical angle i.e.,

$$\theta$$ $$\ge$$ $$\theta$$c = sin$$-$$1(n2 / n1). ........ (1)

Apply Snell's law for refraction at P to get

n0 sin i = n1 sin(90$$^\circ$$ $$-$$ $$\theta$$) = n1 cos$$\theta$$

= $${n_1}\sqrt {1 - {{\sin }^2}\theta } $$. ...... (2)

From equation (2), the angle of incidence is maximum (i = im) when $$\theta$$ is minimum i.e., when $$\theta$$ = $$\theta$$c (from equation (1)). Thus, the numerical aperture is given by

$$NA = \sin {i_m} = {{{n_1}\sqrt {1 - {{\sin }^2}{\theta _c}} } \over {{n_0}}} = {{\sqrt {n_1^2 - n_2^2} } \over {{n_0}}}$$ ........ (3)

Substitute $${n_1} = \sqrt {45} /4$$ and $${n_2} = 3/2$$ in equation (3) to get the numerical aperture for the structure S1 is

$$N{A_1} = {{\sqrt {45/16 - 9/4} } \over {{n_0}}} = {3 \over {4{n_0}}}$$ ...... (4)

Similarly, substitute n1 = 8/4 and n2 = 7/5 in equation (3) to get the numerical aperture for the structure S2 as

$$N{A_2} = {{\sqrt {64/25 - 49/25} } \over {{n_0}}} = {{\sqrt {15} } \over {5{n_0}}}$$ ...... (5)

In case (A), substitute n0 = 4/3 in equation (4) to get NA1 = 9/16 and substitute n0 = 16/3$$\sqrt15$$ in equation (5) to get NA2 = 9/16.

In case (B), substitute n0 = 6/$$\sqrt15$$ in equation (4) to get NA1 = $$\sqrt15$$/8 and substitute n0 = 4/3 in equation (5) to get NA2 = 3$$\sqrt15$$/20.

In case (C), substitute n0 = 1 in equation (4) to get NA1 = 3/4 and substitute n0 = 4/$$\sqrt15$$ equation (5) to get NA2 = 3/4.

In case (D), substitute n0 = 1 in equation (4) to get NA1 = 3/4 and substitute n0 = 4/3 equation (5) to get NA2 = 3$$\sqrt15$$/20.

Comments (0)

Advertisement