JEE Advance - Physics (2015 - Paper 2 Offline - No. 16)
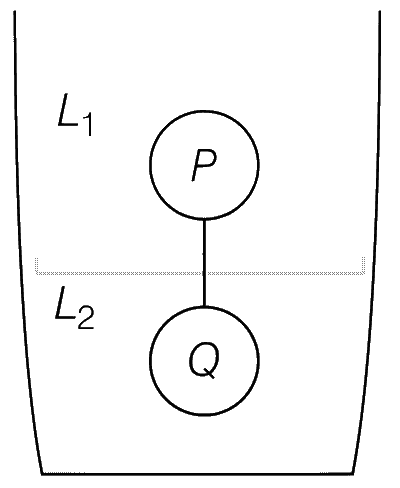
Two spheres P and Q for equal radii have densities $$\rho$$1 and $$\rho$$2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities $$\sigma$$1 and $$\sigma$$2 and viscosities $${\eta _1}$$ and $${\eta _2}$$, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut (see figure) If sphere P along in L2 has terminal velocity vP and Q alone in L1 ha terminal velocity vQ, then

$${{|{v_P}|} \over {|{v_Q}|}} = {{{\eta _1}} \over {{\eta _2}}}$$
$${{|{v_P}|} \over {|{v_Q}|}} = {{{\eta _2}} \over {{\eta _1}}}$$
vP . vQ > 0
vP . vQ < 0
Explanation
Let $V=\frac{4}{3} \pi r^3$ be the volume of the spheres $P$ and $Q$ of equal radii $r$. The forces acting on the sphere $P$ are its weight $\rho_1 V g$, tension from the string $T$, and the buoyancy force $\sigma_1 V g$.

Similarly, forces on the sphere $Q$ are $\rho_2 V g, T$, and $\sigma_1 V g$. In equilibrium, the net force on the spheres $P$ and $Q$ are separately zero i.e.,
$$ \begin{aligned} & T+\rho_1 V g=\sigma_1 V g .........(1) \\\\ & T+\sigma_2 V g=\rho_2 V g ..........(2) \end{aligned} $$
The tension $T > 0$ because the string is taut. Thus, equation (1) gives $\rho_1<\sigma_1$ and equation (2) gives $\rho_2>$ $\sigma_2$. Eliminate $T$ from equations (1) and (2) to get
$$ \sigma_1-\rho_1=\rho_2-\sigma_2 $$ ..........(3)

Now, consider the situation when the sphere $P$ moves in liquid $L_2$ and the sphere $Q$ moves in liquid $L_1$. These spheres will attain the terminal velocities $\vec{v}_{\mathrm{P}}$ and $\vec{v}_{\mathrm{Q}}$ after some time. The direction of the velocity (upwards or downwards) will depend on the density of the sphere in comparison to the density of the liquid. Let us consider the case when $\rho_1>\sigma_2$. In this case, the velocity of the sphere $P$ is downwards. From equation (3), if $\rho_1>\sigma_2$ then $\rho_2<\sigma_1$. If the density of a sphere is less than the density of the liquid in which it is immersed, it will move up. Thus, the velocity of the sphere $Q$ is upwards i.e., the directions of $\vec{v}_{\mathrm{P}}$ and $\vec{v}_{\mathrm{Q}}$ are opposite.
Hence, $\vec{v}_{\mathrm{P}} \cdot \vec{v}_{\mathrm{Q}}<0$.
The forces on the sphere $P$ are its weight $\rho_1 V g$, buoyancy force $\sigma_2 V g$, and viscous drag $6 \pi \eta_2 r v_{\mathrm{P}}$ (see figure). Similarly, the forces on the sphere $Q$ are $\rho_2 V g, \sigma_1 V g$ and $6 \pi \eta_1 r v_{\mathrm{Q}}$. Net forces on the spheres are zero when they move with terminal velocities i.e.,
$$ \begin{aligned} & 6 \pi \eta_2 r v_{\mathrm{P}}+\rho_1 V g=\sigma_2 V g ...........(4) \\\\ & 6 \pi \eta_1 r v_{\mathrm{Q}}+\sigma_2 V g=\rho_1 V g ..........(5) \end{aligned} $$
Solving equations (4) and (5), we get
$$ \begin{aligned} & v_{\mathrm{P}}=\frac{2 r^2\left(\rho_1-\sigma_2\right)}{9 \eta_2} .........(6) \\\\ & v_{\mathrm{Q}}=\frac{2 r^2\left(\sigma_1-\rho_2\right)}{9 \eta_1} .........(7) \end{aligned} $$
By dividing equation (6) by (7), we get
$$ \frac{\left|\vec{v}_{\mathrm{P}}\right|}{\left|\vec{v}_{\mathrm{Q}}\right|}=\frac{\eta_1}{\eta_2} \frac{\rho_1-\sigma_2}{\sigma_2-\rho_2}=\frac{\eta_1}{\eta_2} . $$

Similarly, forces on the sphere $Q$ are $\rho_2 V g, T$, and $\sigma_1 V g$. In equilibrium, the net force on the spheres $P$ and $Q$ are separately zero i.e.,
$$ \begin{aligned} & T+\rho_1 V g=\sigma_1 V g .........(1) \\\\ & T+\sigma_2 V g=\rho_2 V g ..........(2) \end{aligned} $$
The tension $T > 0$ because the string is taut. Thus, equation (1) gives $\rho_1<\sigma_1$ and equation (2) gives $\rho_2>$ $\sigma_2$. Eliminate $T$ from equations (1) and (2) to get
$$ \sigma_1-\rho_1=\rho_2-\sigma_2 $$ ..........(3)

Now, consider the situation when the sphere $P$ moves in liquid $L_2$ and the sphere $Q$ moves in liquid $L_1$. These spheres will attain the terminal velocities $\vec{v}_{\mathrm{P}}$ and $\vec{v}_{\mathrm{Q}}$ after some time. The direction of the velocity (upwards or downwards) will depend on the density of the sphere in comparison to the density of the liquid. Let us consider the case when $\rho_1>\sigma_2$. In this case, the velocity of the sphere $P$ is downwards. From equation (3), if $\rho_1>\sigma_2$ then $\rho_2<\sigma_1$. If the density of a sphere is less than the density of the liquid in which it is immersed, it will move up. Thus, the velocity of the sphere $Q$ is upwards i.e., the directions of $\vec{v}_{\mathrm{P}}$ and $\vec{v}_{\mathrm{Q}}$ are opposite.
Hence, $\vec{v}_{\mathrm{P}} \cdot \vec{v}_{\mathrm{Q}}<0$.
The forces on the sphere $P$ are its weight $\rho_1 V g$, buoyancy force $\sigma_2 V g$, and viscous drag $6 \pi \eta_2 r v_{\mathrm{P}}$ (see figure). Similarly, the forces on the sphere $Q$ are $\rho_2 V g, \sigma_1 V g$ and $6 \pi \eta_1 r v_{\mathrm{Q}}$. Net forces on the spheres are zero when they move with terminal velocities i.e.,
$$ \begin{aligned} & 6 \pi \eta_2 r v_{\mathrm{P}}+\rho_1 V g=\sigma_2 V g ...........(4) \\\\ & 6 \pi \eta_1 r v_{\mathrm{Q}}+\sigma_2 V g=\rho_1 V g ..........(5) \end{aligned} $$
Solving equations (4) and (5), we get
$$ \begin{aligned} & v_{\mathrm{P}}=\frac{2 r^2\left(\rho_1-\sigma_2\right)}{9 \eta_2} .........(6) \\\\ & v_{\mathrm{Q}}=\frac{2 r^2\left(\sigma_1-\rho_2\right)}{9 \eta_1} .........(7) \end{aligned} $$
By dividing equation (6) by (7), we get
$$ \frac{\left|\vec{v}_{\mathrm{P}}\right|}{\left|\vec{v}_{\mathrm{Q}}\right|}=\frac{\eta_1}{\eta_2} \frac{\rho_1-\sigma_2}{\sigma_2-\rho_2}=\frac{\eta_1}{\eta_2} . $$
Comments (0)


