JEE Advance - Physics (2015 - Paper 1 Offline - No. 8)
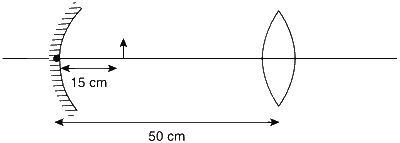
Explanation
Case I
Reflection from mirror
$${1 \over f} = {1 \over v} + {1 \over u} \Rightarrow {1 \over { - 10}} = {1 \over v} + {1 \over { - 15}}$$
$$ \Rightarrow v = - 30$$
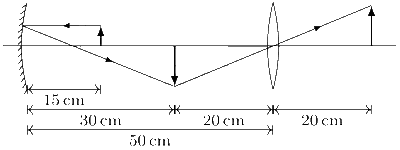
For lens $${1 \over f} = {1 \over v} - {1 \over u}$$
$${1 \over {10}} = {1 \over v} - {1 \over { - 20}}$$
$$v = 20$$
$$\left| {{M_1}} \right| = \left| {{{{v_1}} \over {{u_1}}}} \right|\left| {{{{v_2}} \over {{u_2}}}} \right|$$
$$ = \left( {{{30} \over {15}}} \right)\left( {{{20} \over {20}}} \right)$$
$$ = 2 \times 1 = 2$$ (in air)
Case II :
Now, consider the setup placed in a medium of refractive index $${\mu {'_1}}$$ = 7/6. The focal length of the mirror does not change. Thus, the distance of the image formed by the mirror and its magnification does not change. The focal length of the lens changes. The refractive index of the lens material is $$\mu$$2 = 1.5. Apply lens maker's formula to get the new focal length of the lens
$${1 \over {f'}} = \left( {{{{\mu _2} - \mu {'_1}} \over {\mu {'_1}}}} \right)\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right]$$
$$ = {{{\mu _2} - \mu {'_1}} \over {\mu {'_1}}}{{{\mu _1}} \over {{\mu _2} - {\mu _1}}}{{{\mu _2} - {\mu _1}} \over {{\mu _1}}}\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right]$$
$$ = \left( {{{{\mu _2} - \mu {'_1}} \over {{\mu _2} - {\mu _1}}}} \right)\left( {{{{\mu _1}} \over {\mu {'_1}}}} \right){1 \over f}$$
$$ = \left( {{{1.5 - 7/6} \over {1.5 - 1}}} \right)\left( {{1 \over {7/6}}} \right){1 \over {10}} = {2 \over {35}}$$. ..... (1)
Again using lens formula, $${1 \over v} - {1 \over u} = {1 \over {{f_l}'}}$$
$${1 \over v} - {1 \over { - 20}} = {2 \over {35}} \Rightarrow {1 \over v} = {2 \over {35}} - {1 \over {20}} = {1 \over {140}}$$
$$\therefore$$ v = 140 cm
Magnification, $${m_2}' = {v \over u} = {{140} \over { - 20}} = - 7$$
Magnification produced by the combination,
$${M_2} = {m_1} \times {m_2}' = ( - 2) \times ( - 7) = 14$$
$$\therefore$$ $$\left| {{{{M_2}} \over {{M_1}}}} \right| = {{14} \over 2} = 7$$
Comments (0)


