JEE Advance - Physics (2015 - Paper 1 Offline - No. 18)
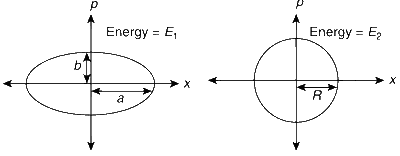
Explanation
1st Particle
P = 0 at x = a $$\Rightarrow$$ 'a' is the amplitude of oscillation 'A1'.
At x = 0, P = b (at mean position)
$$ \Rightarrow m{v_{\max }} = b \Rightarrow {v_{\max }} = {b \over m}$$
$${E_1} = {1 \over 2}mv_{\max }^2 = {m \over 2}{\left[ {{b \over m}} \right]^2} = {{{b^2}} \over {2m}}$$
$${A_1}{\omega _1} = {v_{\max }} = {b \over m}$$
$$ \Rightarrow {\omega _1} = {b \over {ma}} = {1 \over {m{n^2}}}(A = a,\,{a \over b} = {n^2})$$
2nd Particle
P = 0 at x = R $$\Rightarrow$$ A2 = R
At x = 0, P = R $$\Rightarrow$$ $${v_{\max }} = {R \over m}$$
$${E_2} = {1 \over 2}mv_{\max }^2 = {m \over 2}{\left[ {{R \over m}} \right]^2} = {{{R^2}} \over {2m}}$$
$${A_2}{\omega _2} = {R \over m} \Rightarrow {\omega _2} = {R \over {mR}} = {1 \over m}$$
(b) $${{{\omega _2}} \over {{\omega _1}}} = {{1/m} \over {1/m{n^2}}} = {n^2}$$
(c) $${\omega _1}{\omega _2} = {1 \over {m{n^2}}} \times {1 \over m} = {1 \over {{m^2}{n^2}}}$$
(d) $${{{E_1}} \over {{\omega _1}}} = {{{b^2}/2m} \over {1/m{n^2}}} = {{{b^2}{n^2}} \over 2} = {{{a^2}} \over {2{n^2}}} = {{{R^2}} \over 2}$$
$${{{E_2}} \over {{\omega _2}}} = {{{R^2}/2m} \over {1/m}} = {{{R^2}} \over 2}$$
$$ \Rightarrow {{{E_1}} \over {{\omega _1}}} = {{{E_2}} \over {{\omega _2}}}$$
Comments (0)


