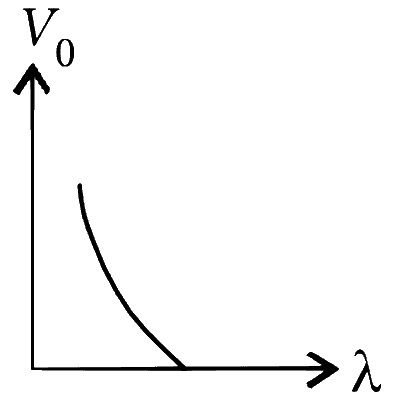
Stopping potential (V₀) is given by

$$e{V_0} = {{hc} \over \lambda } - \phi $$

Graph between V₀ and $$\lambda$$ :

$$e{V_0} + \phi = {{hc} \over \lambda }$$

$$(e{V_0} + \phi )\lambda = hc$$

$$(e{V_0} + \phi )\lambda $$ = constant

Here, both e and $$\phi$$ are also constant. It represents a hyperbola.

For, V₀ = 0, $$\lambda = {{constant} \over \phi } = $$ constant

So correct option is (a).

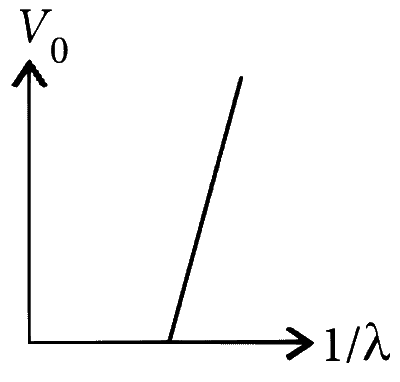
Graph between V₀ and $${1 \over \lambda }$$ :

$${V_0} = \left( {{{hc} \over e}} \right)\left( {{1 \over \lambda }} \right) - \left( {{\phi \over e}} \right)$$

It represents a straight line with slope $$\left( {{{hc} \over e}} \right)$$ and intercept $$\left( { - {\phi \over e}} \right)$$ on V₀ axis.