JEE Advance - Physics (2014 - Paper 2 Offline - No. 9)
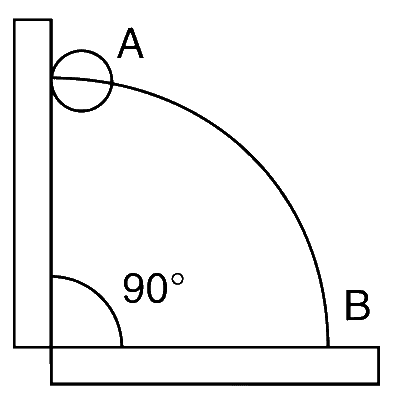
A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the below figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
Explanation
Let v be speed of the bead when it makes an angle $$\theta$$ with the vertical direction.
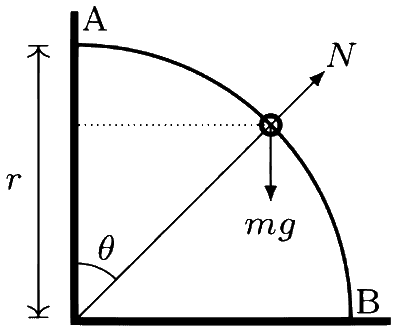
The forces acting on the bead are its weight mg and normal reaction N. Since all the forces acting on the bead are conservative, the mechanical energy of the bead is conserved i.e.,
$$mgr(1 - \cos \theta ) = {1 \over 2}m{v^2}$$ ..... (1)
The radially inward components of force provide centripetal acceleration to the bead i.e.,
$$mg\cos \theta - N = m{v^2}/r$$ ...... (2)
Eliminate v2 from equations (1) and (2) to get
$$N = mg(3\cos \theta - 2)$$ ...... (3)
When 3cos$$\theta$$ > 2, direction of N will be same as shown in figure, i.e., radially outward.
When 3cos$$\theta$$ < 2, direction of N will be radially inward. Now, normal on the bead is opposite to the force applied on the wire by the bead, following Newton's third law. Therefore, the force applied on the bead by the wire is radially inwards initially and radially outwards later, as it moves from A to B.
Comments (0)


