JEE Advance - Physics (2014 - Paper 2 Offline - No. 20)
A block of mass m1 = 1 kg another mass m2 = 2 kg, are placed together (see figure) on an inclined plane with angle of inclination $$\theta$$. Various values of $$\theta$$ are given in List I. The coefficient of friction between the block m1 and the plane is always zero. The coefficient of static and dynamic friction between the block m2 and the plane are equal to $$\mu$$ = 0.3. In List II expressions for the friction on the block m2 are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g.
[Useful information : tan (5.5$$^\circ$$) $$\approx$$ 0.1; tan (11.5$$^\circ$$) $$\approx$$ 0.2; tan (16.5$$^\circ$$) $$\approx$$ 0.3]
| List I | List II | ||
|---|---|---|---|
| P. | $$\theta = 5^\circ $$ |
1. | $${m_2}g\sin \theta $$ |
| Q. | $$\theta = 10^\circ $$ |
2. | $$({m_1} + {m_2})g\sin \theta $$ |
| R. | $$\theta = 15^\circ $$ |
3. | $$\mu {m_2}g\cos \theta $$ |
| S. | $$\theta = 20^\circ $$ |
4. | $$\mu ({m_1} + {m_2})g\cos \theta $$ |
Explanation
The forces on the block of mass m1 are its weight m1g, normal reaction from the inclined plane N1, and the reaction from the second block R.
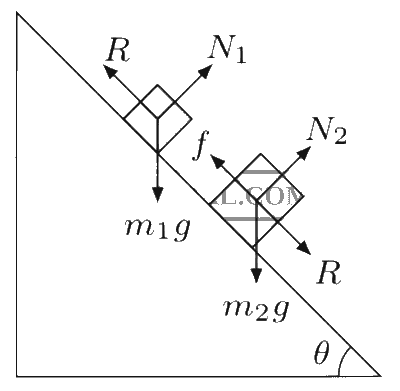
Similarly, forces on the block of mass m2 are m2g, N2, R, and the frictional force f. If $$\theta$$ is slowly increased, f starts increasing and attains its maximum value f = $$\mu$$N2 at $$\theta$$ = $$\theta$$r (angle of repose). The blocks are stationary if $$\theta$$ $$\le$$ $$\theta$$r otherwise they are moving. Consider the limiting case, $$\theta$$ = $$\theta$$r, when the blocks are at rest and
$$f = \mu {N_2}$$ ...... (1)
Apply Newton's second law to m1,
$$R = {m_1}g\sin \theta $$ ....... (2)
$${N_1} = R = {m_2}g\cos \theta $$ ....... (3)
and to m2,
$$f = R + {m_2}g\sin \theta $$ ...... (4)
$${N_2} = {m_1}g\cos \theta $$ ...... (5)
Eliminate R, N2 and f from equations (1)-(5) to get
$${\theta _r} = {\tan ^{ - 1}}\left( {{{\mu {m_2}} \over {{m_1} + {m_2}}}} \right) = {\tan ^{ - 1}}\left( {{{0.3 \times 2} \over {1 + 2}}} \right)$$
$$ = {\tan ^{ - 1}}(0.2) = 11.5^\circ $$
Thus, for $$\theta$$ = 5$$^\circ$$ and $$\theta$$ = 10$$^\circ$$, blocks are at rest with frictional force
$$f = R + {m_2}g\sin \theta = ({m_1} + {m_2})g\sin \theta $$
For $$\theta$$ = 15$$^\circ$$ and $$\theta$$ = 20$$^\circ$$, blocks are moving with frictional force
$$f = \mu {N_2} = \mu {m_2}g\cos \theta $$, (limiting value).
Comments (0)


