JEE Advance - Physics (2014 - Paper 2 Offline - No. 19)
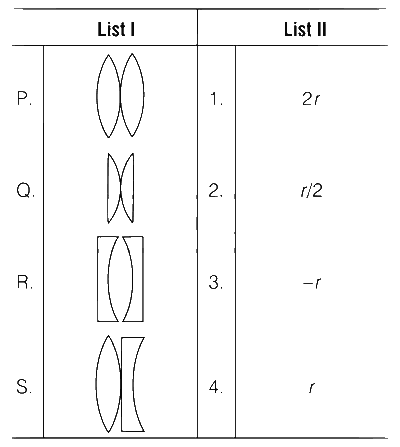
Four combinations of two thin lenses are given in List I. The radius of curvature of all curved surfaces is r and the refractive index of all the lenses is 1.5. Match lens combinations in List I with their focal length in List II and select the correct answer using the code given below the lists.
Explanation
The lens maker's formula gives focal length of the bi-convex lens as
$${1 \over {{f_1}}} = (\mu - 1)\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right]$$
$$ = (1.5 - 1)\left[ {{1 \over r} - {1 \over { - r}}} \right] = {1 \over r}$$ ..... (1)
The focal length of a plano-convex (also convex-plane) lens is given by
$${1 \over {{f_2}}} = (1.5 - 1)\left[ {{1 \over \infty } - {1 \over { - r}}} \right] = {1 \over {2r}}$$ ...... (2)
and that of a plano-concave (also concave-plano) lens is given by
$${1 \over {{f_3}}} = (1.5 - 1)\left[ {{1 \over \infty } - {1 \over r}} \right] = - {1 \over {2r}}$$ ..... (3)
Case P:
Therefore, $${1 \over {{f_{eff}}}} = {1 \over r} + {1 \over r}$$
$${f_{eff}} = {r \over 2}$$
(P) $$\to$$ (2)
Case Q :
$${1 \over {{f_{eff}}}} = {1 \over {2r}} + {1 \over {2r}}$$
$${f_{eff}} = r$$
(Q) $$\to$$ (4)
Case R :
$${1 \over {{f_{eff}}}} = - {1 \over {2r}} - {1 \over {2r}}$$
$${f_{eff}} = - r$$
(R) $$\to$$ (3)
Case S : $${1 \over {{f_{eff}}}} = {1 \over r} - {1 \over {2r}} = {1 \over {2r}}$$
$${f_{eff}} = 2r$$
(S) $$\to$$ (1)
Comments (0)


