JEE Advance - Physics (2014 - Paper 2 Offline - No. 17)
If the density of air is $$\rho$$a and that of the liquid $$\rho$$l, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to
$\sqrt{\frac{\rho_a}{\rho_{\ell}}}$
$\sqrt{\rho_a \rho_{\ell}}$
$\sqrt{\frac{\rho_{\ell}}{\rho_a}}$
$\rho_{\ell}$
Explanation
For horizontal flow, Bernoulli's theorem becomes
$${P \over \rho } + gh + {1 \over 2}{v^2} = k'$$
$$P + {1 \over 2}\rho {v^2} = k$$ (h = 0)
Between points 1 and 2 :
$${P_1} - {P_2} = {1 \over 2}{\rho _a}v_a^2$$
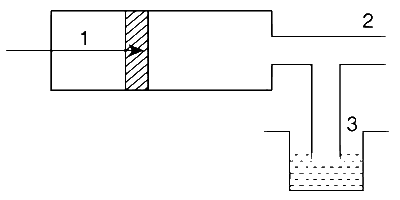
Between points 2 and 3 :
$${P_3} - {P_2} = {1 \over 2}{\rho _l}v_l^2$$
Since, P1 = P3, we have
$${1 \over 2}{\rho _l}v_l^2 = {1 \over 2}{\rho _a}v_a^2$$
$${{{v_l}} \over {{v_a}}} =\sqrt {{{{\rho _a}} \over {{\rho _l}}}} $$
Comments (0)



