Sign In

JEE Advance - Physics (2014 - Paper 2 Offline - No. 12)

The figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper. The distance of each wire from the centre of the loop is d. The loop and the wires are carrying the same current I. The current in the loop is in the counter clockwise direction if seen from above.

The figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper. The distance of each wire from the centre of the loop is d. The loop and the wires are carrying the same current I. The current in the loop is in the counter clockwise direction if seen from above.

The figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper. The distance of each wire from the centre of the loop is d. The loop and the wires are carrying the same current I. The current in the loop is in the counter clockwise direction if seen from above.

When d $$\approx$$ a but wires are not touching the loop, it is found that the net magnetic field on the axis of the loop is zero at a height h above the loop. In that case
current in wire 1 and wire 2 is the direction PQ and RS, respectively, and h $$\approx$$ a.
current in wire 1 and wire 2 is the direction PQ and SR, respectively, and h $$\approx$$ a.
current in wire 1 and wire 2 is the direction PQ and SR, respectively, and h $$\approx$$ 1.2a.
current in wire 1 and wire 2 is the direction PQ and RS, respectively, and h $$\approx$$ 1.2a.

Explanation

BR = B due to ring

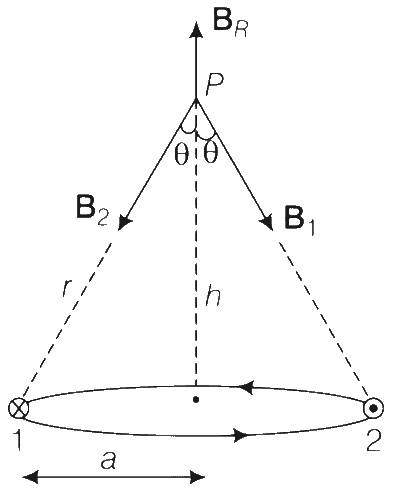
JEE Advanced 2014 Paper 2 Offline Physics - Magnetism Question 26 English Explanation

B1 = B due to wire-1

B2 = B due to wire-2

In magnitudes

$${B_1} = {B_2} = {{{\mu _0}I} \over {2\pi r}}$$

Resultant of B1 and B2

$$ = 2{B_1}\cos \theta = 2\left( {{{{\mu _0}I} \over {2\pi r}}} \right)\left( {{h \over r}} \right)$$

$$ = {{{\mu _0}Ih} \over {\pi {r^2}}}$$

$${B_R} = {{{\mu _0}I{R^2}} \over {2{{({R^2} + {x^2})}^{3/2}}}}$$

$$ = {{2{\mu _0}I\pi {a^2}} \over {4\pi {r^3}}}$$

As, R = a, x = h and a2 + h2 = r2

For zero magnetic field at P,

$${{{\mu _0}Ih} \over {\pi {r^2}}} = {{2{\mu _0}I\pi {a^2}} \over {4\pi {r^3}}}$$

$$ \Rightarrow \pi {a^2} = 2rh \Rightarrow h \approx 1.2a$$

Comments (0)

Advertisement