Sign In

JEE Advance - Physics (2014 - Paper 2 Offline - No. 1)

Charges $$Q,$$ $$2Q$$ and $$4Q$$ are uniformly distributed in three dielectric solid spheres $$1,2$$ and $$3$$ of radii $$R/2,R$$ and $$2R$$ respectively, as shown in figure. If magnitude of the electric fields at point $$P$$ at a distance $$R$$ from the center of sphere $$1,2$$ and $$3$$ are $${E_1}$$, $${E_2}$$ and $${E_3}$$ respectively, then
JEE Advanced 2014 Paper 2 Offline Physics - Electrostatics Question 53 English 1
JEE Advanced 2014 Paper 2 Offline Physics - Electrostatics Question 53 English 2
$${E_1} > {E_2} > {E_3}$$
$${E_3} > {E_1} > {E_2}$$
$${E_2} > {E_1} > {E_3}$$
$${E_3} > {E_2} > {E_1}$$

Explanation

Electric field due to uniformly charged dielectric solid sphere of radius R at a point P is given by

JEE Advanced 2014 Paper 2 Offline Physics - Electrostatics Question 53 English Explanation

$$E = \left\{ {\matrix{ {k\,.\,{Q \over {{R^3}}}\,.\,r,} & {r \le R} \cr {k\,.\,{Q \over {{r^2}}},} & {r > R} \cr } } \right.$$

In first two cases, P is outside the sphere. Therefore,

$${E_1} = {1 \over {4\pi {E_0}}}.\,{Q \over {{R^2}}}$$ ..... (1)

$${E_2} = {1 \over {4\pi {E_0}}}.\,{{2Q} \over {{R^2}}}$$ .... (2)

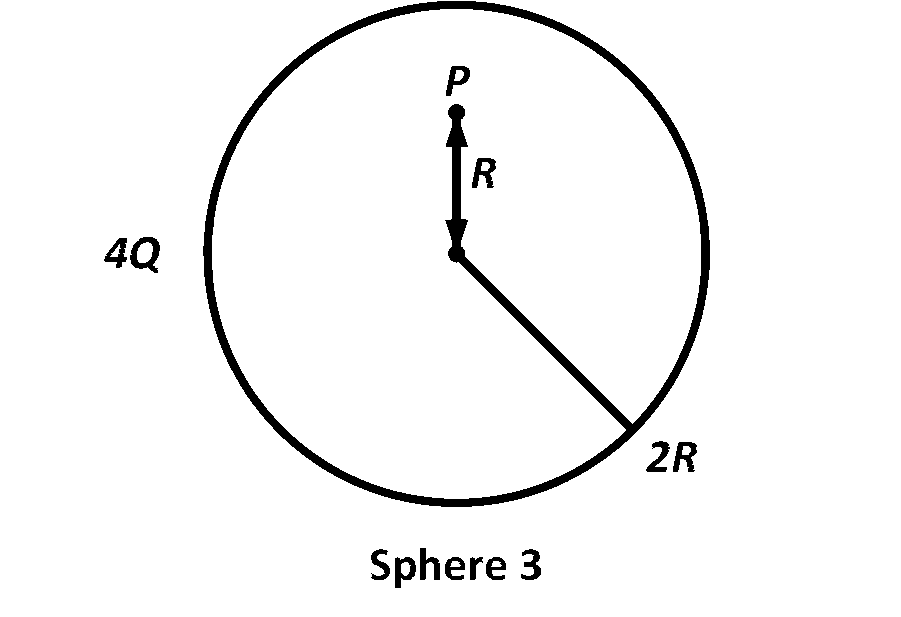
In Sphere 3, point P located is inside. Therefore,

$${E_3} = \left( {{\rho \over {3{E_0}}}} \right)r$$

$$\rho = {{4Q} \over {(4/3)\pi {{(2R)}^3}}}$$

$$ = {{12Q} \over {4\pi \,.\,8{R^3}}} = {{3Q} \over {8\pi }}$$

$${E_3} = \left( {{{3Q} \over {\pi {R^3}}}} \right)R$$

$${E_3} = {1 \over {4\pi {E_0}}}\,.\,{Q \over {2{R^2}}}$$ ..... (3)

$${E_2} > {E_1} > {E_3}$$

Comments (0)

Advertisement