JEE Advance - Physics (2014 - Paper 1 Offline - No. 8)
At time t = 0, terminal A in the circuit shown in the figure is connected to B by a key and an alternating current I(t) = I0 cos ($$\omega$$t), with I0 = 1 A and $$\omega$$ = 500 rad s-1 starts flowing in it with the initial direction shown in the figure. At $$t = {{7\pi } \over {6\omega }}$$, the key is switched from B to D. Now onwards only A and D are connected. A total charge Q flows from the battery to charge the capacitor fully. If C = 20 $$\mu$$F, R = 10 $$\Omega$$ and the battery is ideal with emf of 50 V, identify the correct statement(s).
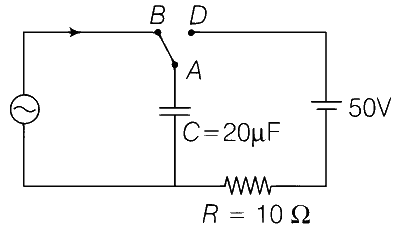

Magnitude of the maximum charge on the capacitor before $$t = {{7\pi } \over {6\omega }}$$ is 1 $$\times$$ 10$$-$$3 C
The current in the left part of the circuit just before $$t = {{7\pi } \over {6\omega }}$$ is clockwise
Immediately after A is connected to D, the current in R is 10 A
Q = 2 $$\times$$ 10$$-$$3 C
Explanation
The current flowing through the capacitor and its charge are given by
$$i = {i_0}\cos \omega t$$, .... (1)
$$Q = \int {idt = \int {{i_0}\cos \omega t\,dt = {{{i_0}} \over \omega }\sin \omega t + k} } $$ $$ = {{{i_0}} \over \omega }\sin \omega t$$, ...... (2)
where we have used the initial condition, Q = 0 at t = 0, to get the integration constant k = 0. The charge attains the maximum value Qmax at t = $$\pi$$ / (2$$\omega$$),
Qmax = i0/$$\omega$$ = 1/500 = 2 $$\times$$ 10$$-$$3 C.
The key is switched from B to D at the time t = 7$$\pi$$/6$$\omega$$. Substitute t = 7$$\pi$$/6$$\omega$$ in equations (1) and (2) to get current and charge
i = i0 cos(7$$\pi$$/6) = cos($$\pi$$ + $$\pi$$/6) = $$-$$ cos($$\pi$$/6)
$$ = - \sqrt 3 /2$$ A,
Qi = (i0/$$\omega$$) sin(7$$\pi$$/6) = 2 $$\times$$ 10$$-$$3 sin($$\pi$$ + $$\pi$$/6)
= $$-$$ 1 $$\times$$ 10$$-$$3 C.
Note that negative sign in i indicates the counterclockwise direction of current and negative sign in Qi indicates the negative charge on the upper plate.
The potential across the capacitor is $${V_C} = {{{Q_i}} \over C} = - {{1 \times {{10}^{ - 3}}} \over {20 \times {{10}^{ - 6}}}}$$ = $$-$$ 50 V (upper plate at lower potential). Immediately after A is connected to D, the potential across the resistor is VR = 100 V and hence the current through it is i = VR/R = 100/10 = 10 A (counterclockwise). The potential across the capacitor when it is fully charged is equal to the battery emf. Thus, the charge on the capacitor in fully charged condition is
Qf = V/C = 50/(20 $$\times$$ 10$$-$$6) = 1 $$\times$$ 10$$-$$3 C.
The sign of Qf indicates the positive charge on the upper plate. Hence, charge that flows through the battery is
Q = Qf $$-$$ Qi = 1 $$\times$$ 10$$-$$3 $$-$$ ($$-$$ 1 $$\times$$ 10$$-$$3) = 2 $$\times$$ 10$$-$$3 C.
$$i = {i_0}\cos \omega t$$, .... (1)
$$Q = \int {idt = \int {{i_0}\cos \omega t\,dt = {{{i_0}} \over \omega }\sin \omega t + k} } $$ $$ = {{{i_0}} \over \omega }\sin \omega t$$, ...... (2)
where we have used the initial condition, Q = 0 at t = 0, to get the integration constant k = 0. The charge attains the maximum value Qmax at t = $$\pi$$ / (2$$\omega$$),
Qmax = i0/$$\omega$$ = 1/500 = 2 $$\times$$ 10$$-$$3 C.
The key is switched from B to D at the time t = 7$$\pi$$/6$$\omega$$. Substitute t = 7$$\pi$$/6$$\omega$$ in equations (1) and (2) to get current and charge
i = i0 cos(7$$\pi$$/6) = cos($$\pi$$ + $$\pi$$/6) = $$-$$ cos($$\pi$$/6)
$$ = - \sqrt 3 /2$$ A,
Qi = (i0/$$\omega$$) sin(7$$\pi$$/6) = 2 $$\times$$ 10$$-$$3 sin($$\pi$$ + $$\pi$$/6)
= $$-$$ 1 $$\times$$ 10$$-$$3 C.
Note that negative sign in i indicates the counterclockwise direction of current and negative sign in Qi indicates the negative charge on the upper plate.
The potential across the capacitor is $${V_C} = {{{Q_i}} \over C} = - {{1 \times {{10}^{ - 3}}} \over {20 \times {{10}^{ - 6}}}}$$ = $$-$$ 50 V (upper plate at lower potential). Immediately after A is connected to D, the potential across the resistor is VR = 100 V and hence the current through it is i = VR/R = 100/10 = 10 A (counterclockwise). The potential across the capacitor when it is fully charged is equal to the battery emf. Thus, the charge on the capacitor in fully charged condition is
Qf = V/C = 50/(20 $$\times$$ 10$$-$$6) = 1 $$\times$$ 10$$-$$3 C.
The sign of Qf indicates the positive charge on the upper plate. Hence, charge that flows through the battery is
Q = Qf $$-$$ Qi = 1 $$\times$$ 10$$-$$3 $$-$$ ($$-$$ 1 $$\times$$ 10$$-$$3) = 2 $$\times$$ 10$$-$$3 C.
Comments (0)


