JEE Advance - Physics (2014 - Paper 1 Offline - No. 5)
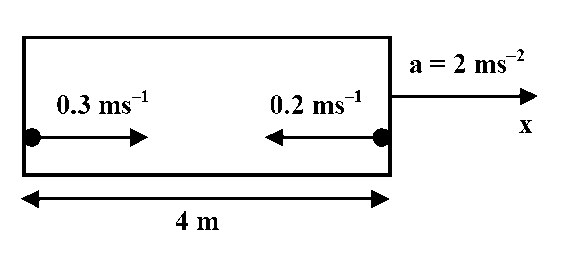
Explanation
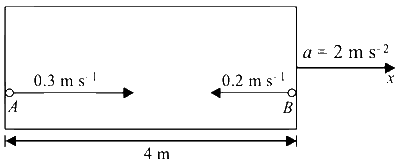
Consider the motion of two balls with respect to rocket.
Distance travelled by ball A from left end of the chamber is
$$ = {{{u^2}} \over {2a}} = {{{{(0.3)}^2}} \over {2 \times 2}} = {{0.09} \over 4} \approx 0.02$$ m
So, collision of two balls will take place very near to left end of the chamber.
For ball B
$$S = ut{1 \over 2}a{t^2}$$
$$ - 4 = - 0.2 \times t - {1 \over 2} \times 2 \times {t^2}$$
$${t^2} + 0.2t - 4 = 0$$
$$t = {{ - 0.2 \pm \sqrt {{{(0.2)}^2} - 4(1)( - 4)} } \over 2} = {{ - 0.2 \pm \sqrt {0.04 + 16} } \over 2}$$
t = 1.9 s, $$-$$2.1 s
Since t can't be negative
$$\therefore$$ t = 1.9 s
Nearest integer is 2 s.
Also, from
$$S = ut + {1 \over 2}a{t^2}$$
$${S_A} = 0.3t + {1 \over 2}( - 2){t^2} = 0.3t - {t^2}$$
$${S_B} = 0.2t + {1 \over 2}(2){t^2} = 0.2t + {t^2}$$
$$\because$$ $${S_A} + {S_B} = 4$$
$$\Rightarrow$$ 0.5 t = 4 or t = 8 s
Comments (0)


