Sign In

JEE Advance - Physics (2014 - Paper 1 Offline - No. 2)

A parallel plate capacitor has a dielectric slab of dielectric constant $$K$$ between its plates that covers $$1/3$$ of the area of its plates, as shown in the figure. The total capacitance of the capacitor is $$C$$ while that of the portion with dielectric in between is $${C_1}.$$ When the capacitor is charged, the plate area covered by the dielectric gets charge $${Q_1}$$ and the rest of the area gets charge $${Q_2}.$$ The electric field in the dielectric is $${E_1}$$ and that in the other portion is $${E_2}.$$ Choose the correct option/ options, ignoring edge effects.

JEE Advanced 2014 Paper 1 Offline Physics - Capacitor Question 14 English
$${{{E_1}} \over {{E_2}}} = 1$$
$${{{E_1}} \over {{E_2}}} = {1 \over K}$$
$${{{Q_1}} \over {{Q_2}}} = {3 \over K}$$
$${C \over {{C_1}}} = {{2 + K} \over K}$$

Explanation

JEE Advanced 2014 Paper 1 Offline Physics - Capacitor Question 14 English Explanation

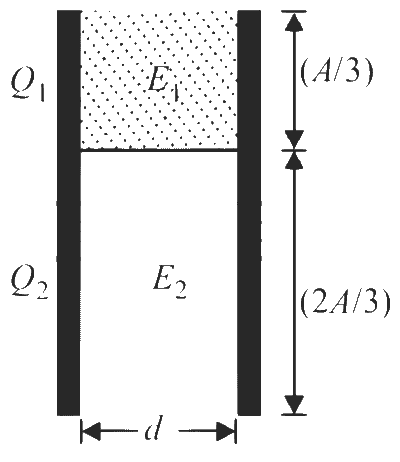
Let A be area of each plate and d is the distance between the plates.

The given capacitor is equivalent to two capacitors in parallel with capacitances

$${C_1} = {{K{\varepsilon _0}(A/3)} \over d} = {{K{\varepsilon _0}A} \over {3d}}$$

$${C_2} = {{{\varepsilon _0}(2A/3)} \over d} = {{2{\varepsilon _0}A} \over {3d}}$$

$$\therefore$$ $$C = {C_1} + {C_2}$$

$$ = {{K{\varepsilon _0}A} \over {3d}} + {{2{\varepsilon _0}A} \over {3d}} = {{{\varepsilon _0}A} \over {3d}}(K + 2)$$

$$\therefore$$ $${C \over {{C_1}}} = {{K + 2} \over K}$$

Hence, option (d) is correct.

Let V be potential difference between the plates. Then

$${E_1} = {V \over d}$$ and $${E_2} = {V \over d}$$

$$\therefore$$ $${{{E_1}} \over {{E_2}}} = 1$$

Hence, option (a) is correct and option (b) is incorrect.

$${Q_1} = {C_1}V = {{K{\varepsilon _0}A} \over {3d}}V$$ and $${Q_2} = {C_2}V = {{2{\varepsilon _0}A} \over {3d}}V$$

$$\therefore$$ $${{{Q_1}} \over {{Q_2}}} = {K \over 2}$$

Hence, option (c) is incorrect.

Comments (0)

Advertisement