JEE Advance - Physics (2014 - Paper 1 Offline - No. 17)
Two parallel wires in the plane of the paper are distance X0 apart. A point charge is moving with speed u between the wires in the same plane at a distance X1 from one of the wires. When the wires carry current of magnitude I in the same direction, the radius of curvature of the path of the point charge is R1. In contrast, if the currents I in the two wires have directions opposite to each other, the radius of curvature of the path is R2. If $${{{X_0}} \over {{X_1}}} = 3$$, and value of R1/R2 is
Answer
3
Explanation
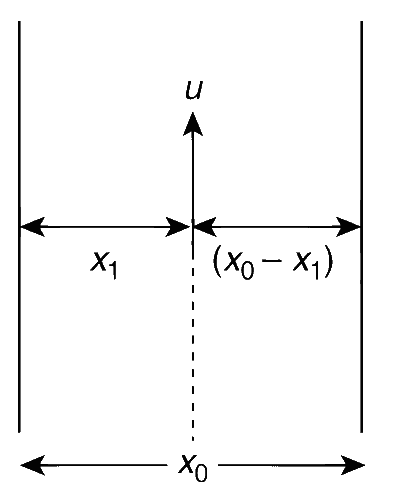
When current in wires is in same direction, the magnetic fields due to two wires all in opposite direction.
From $$B = {{{\mu _0}} \over {4\pi }}.{{2I} \over r}$$, we get
$${B_1} = {{{\mu _0}} \over {4\pi }}.2I\left[ {{1 \over {{x_1}}} - {1 \over {({x_0} - {x_1})}}} \right]$$
$$ = {{{\mu _0}I} \over {2\pi }}\left[ {{{{x_0} - {x_1} - {x_1}} \over {{x_1}({x_0} - {x_1})}}} \right]$$
$$ = {{{\mu _0}I} \over {2\pi }}\left[ {{{{x_0} - 2{x_1}} \over {{x_1}({x_0} - {x_1})}}} \right]$$ ..... (1)
When the direction of current in two wires is opposite, field will be in the same direction.
$${B_2} = {{{\mu _0}I} \over {2\pi }}\left[ {{1 \over {{x_1}}} + {1 \over {({x_0} - {x_1})}}} \right]$$
$${B_2} = {{{\mu _0}I} \over {2\pi }}\left[ {{{{x_0} - {x_1} + {x_1}} \over {{x_1}({x_0} - {x_1})}}} \right]$$
$${B_2} = {{{\mu _0}I} \over {2\pi }}\left[ {{{{x_0}} \over {{x_1}({x_0} - {x_1})}}} \right]$$
From $${{m{v^2}} \over r} = qvB$$ or $$v = {{qBr} \over m}$$ or $$r = {{mv} \over {qB}}$$
$$B \propto {1 \over r}$$
Therefore, $${{{R_1}} \over {{R_2}}} = {{{B_2}} \over {{B_1}}} = {{{x_0}} \over {({x_0} - 2{x_1})}}$$
$${{{R_1}} \over {{R_2}}} = {{{x_0}/{x_1}} \over {({x_0}/{x_1}) - (2{x_1}/{x_1})}} = {3 \over {3 - 2}} = 3$$
Comments (0)


