JEE Advance - Physics (2014 - Paper 1 Offline - No. 16)
A uniform circular disc of mass 1.5 kg and radius 0.5 m is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude F = 0.5 N are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure). One second after applying the forces, the angular speed of the disc in rad s-1 is
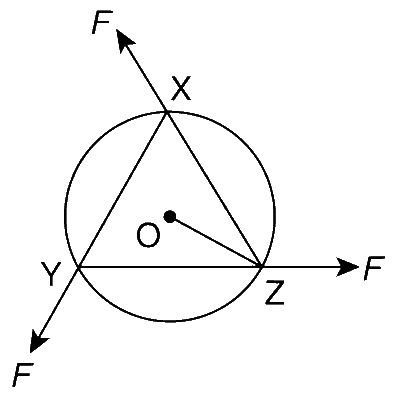

Answer
2
Explanation
In triangle OZP, the distances OZ = R and OP = R sin30$$^\circ$$ = R/2.
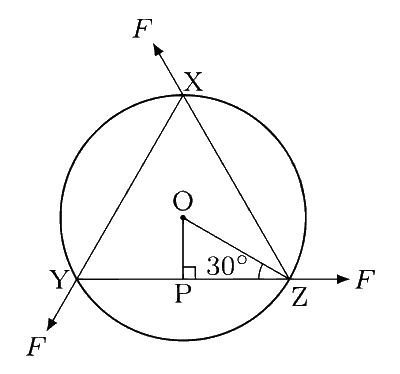
The total torque by the three forces about the centre of mass O is
$$\tau$$ = 3F| OP | = 3F R/2.
The monent of inertia of the disc about the axis of rotation is $$I = {1 \over 2}M{R^2}$$. Using $$\tau$$ = I$$\alpha$$, we get
$$\alpha = {\tau \over I} = {{3F} \over {MR}} = {{3 \times 0.5} \over {1.5 \times 0.5}} = 2$$ rad/s2.
The angular velocity after t = 1 is given by
$$\omega = {\omega _0} + \alpha t = 0 + 2 \times 1 = 2$$ rad/s.

The total torque by the three forces about the centre of mass O is
$$\tau$$ = 3F| OP | = 3F R/2.
The monent of inertia of the disc about the axis of rotation is $$I = {1 \over 2}M{R^2}$$. Using $$\tau$$ = I$$\alpha$$, we get
$$\alpha = {\tau \over I} = {{3F} \over {MR}} = {{3 \times 0.5} \over {1.5 \times 0.5}} = 2$$ rad/s2.
The angular velocity after t = 1 is given by
$$\omega = {\omega _0} + \alpha t = 0 + 2 \times 1 = 2$$ rad/s.
Comments (0)


