JEE Advance - Physics (2014 - Paper 1 Offline - No. 15)
Two ideal batteries of emf V1 and V2 and three resistances R1, R2 and R3 are connected as shown in the figure. The current in resistance R2 would be zero if
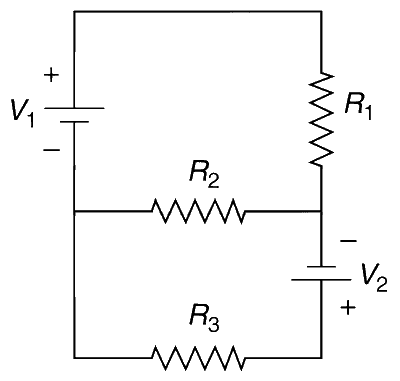

V1 = V2 and R1 = R2 = R3
V1 = V2 and R1 = 2R2 = R3
V1 = 2V2 and 2R1 = 2R2 = R3
2V1 = V2 and 2R1 = R2 = R3
Explanation
Let i1 and i2 be the currents as shown in the figure.
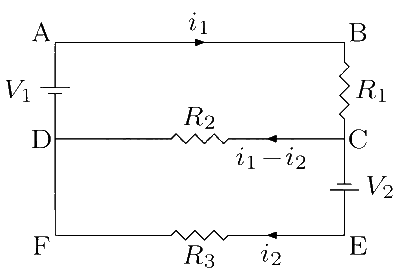
Apply Kirchhoff's law in the loop ABCDA and CEFDC to get
$${i_1}{R_1} + ({i_1} - {i_2}){R_2} = {V_1}$$ ..... (1)
$${i_2}{R_3} - ({i_1} - {i_2}){R_2} = {V_2}$$ ...... (2)
Multiply equation (1) by R3 and (2) by R1 and then subtract to get the current through R2 as
$$({i_1} - {i_2}) = {{{V_1}{R_3} - {V_2}{R_1}} \over {{R_1}{R_3} + {R_2}{R_3} - {R_1}{R_2}}}$$.
The current through R2 becomes zero when V1R3 = V2R1.

Apply Kirchhoff's law in the loop ABCDA and CEFDC to get
$${i_1}{R_1} + ({i_1} - {i_2}){R_2} = {V_1}$$ ..... (1)
$${i_2}{R_3} - ({i_1} - {i_2}){R_2} = {V_2}$$ ...... (2)
Multiply equation (1) by R3 and (2) by R1 and then subtract to get the current through R2 as
$$({i_1} - {i_2}) = {{{V_1}{R_3} - {V_2}{R_1}} \over {{R_1}{R_3} + {R_2}{R_3} - {R_1}{R_2}}}$$.
The current through R2 becomes zero when V1R3 = V2R1.
Comments (0)


