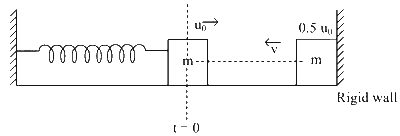
Here we will apply the concept of energy conservation and concept of SHM.

We know that for elastic collision, coefficient of restitution, e = 1

Hence, $$e = {v \over {0.5{u_0}}} = 1 \Rightarrow v = 0.5{u_0}$$

Therefore, particle rebounds with the same speed after collision.

Now, by energy conservation of the spring-mass system, we can say that the speed of the particle when it returns to its equilibrium position is $$u_0$$.

By SHM,

$$v = {v_{\max }}\cos wt$$

$$ \Rightarrow 0.5{u_0} = {u_0}\cos \left( {\sqrt {{K \over m}} t} \right)$$

$$ \Rightarrow {1 \over 2} = \cos \left( {\sqrt {{K \over m}} t} \right)$$

$$ \Rightarrow {\pi \over 3} = \sqrt {{K \over m}} t$$

$$ \Rightarrow t = {\pi \over 3}\sqrt {{m \over K}} $$

Hence, time taken by the particle to reach the wall is $${\pi \over 3}\sqrt {{m \over K}} $$

So the time at which the particle passes through the equilibrium position for the first time is

$$2t = {{2\pi } \over 3}\sqrt {{m \over K}} $$

The time at which the maximum compression of the spring occurs is

$$t' = 2t + {T \over 4} = {{2\pi } \over 3}\sqrt {{m \over K}} + {{2\pi } \over 4}\sqrt {{m \over K}} $$

$$ = \left( {{2 \over 3} + {1 \over 2}} \right)\pi \sqrt {{m \over K}} $$

$$t' = {{7\pi } \over 6}\sqrt {{m \over K}} $$

The time at which the particle passes through the equilibrium position for the second time is

$$ = t' + T$$

$$ = {{7\pi } \over 6}\sqrt {{m \over K}} + {\pi \over 2}\sqrt {{m \over K}} $$

$$ = \left( {{{7\pi } \over 6} + {\pi \over 2}} \right)\sqrt {{m \over K}} = {{10\pi } \over 6}\sqrt {{m \over K}} $$

$$ = {{5\pi } \over 3}\sqrt {{m \over K}} $$

Hence, options (A) and (D) are correct.