JEE Advance - Physics (2013 - Paper 2 Offline - No. 19)
One mole of a monatomic ideal gas is taken along two cyclic processes E $$\to$$ F $$\to$$ G $$\to$$ E and E $$\to$$ F $$\to$$ H $$\to$$ E as shown in the PV diagram. The processes involved are purely isochoric, isobaric, isothermal or adiabatic.
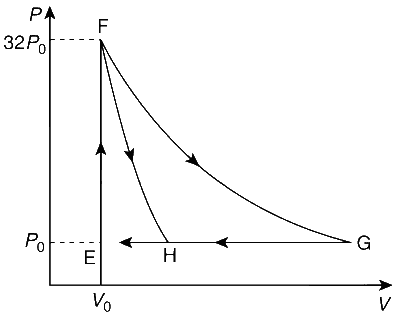
Match the paths in List I with the magnitudes of the work done in List II and select the correct answer using the codes given below the lists :
| List I | List II | ||
|---|---|---|---|
| P. | $$G \to E$$ |
1. | 160$${P_0}{V_0}$$ln2 |
| Q. | $$G \to H$$ |
2. | 36$${P_0}{V_0}$$ |
| R. | $$F \to H$$ |
3. | 24$${P_0}{V_0}$$ |
| S. | $$F \to G$$ |
4. | 31$${P_0}{V_0}$$ |
Explanation
From the given figure, it can be concluded that process FG is isothermal and process FH is adiabatic.
$${\gamma _{mono}} = 1 + {2 \over f} = {5 \over 3}$$
$${P_0}V_G^{5/3} = 32{P_0}V_0^{5/3}$$
$${V_G} = {(32)^{3/5}}{V_0} = 8{V_0}$$
$$\Delta {W_{GE}} = {P_0}({V_0} - 32{V_0}) = - 31{P_0}{V_0}$$
Thus, the correct mapping is (P) $$\to$$ (4).
$$\Delta {W_{GH}} = {P_0}(8{V_0} - 32{V_0}) = - 24{P_0}{V_0}$$
Thus, the correct mapping is (Q) $$\to$$ (3).
$$\Delta {W_{FH}} = {{{P_0}(8{V_0}) - 32{P_0}{V_0}} \over {1 - (5/3)}} = {{ - 24{P_0}{V_0}} \over { - (2/3)}} = 36{P_0}{V_0}$$
Thus the correct mapping is (R) $$\to$$ (2).
$$\Delta {W_{FG}} = 32R{T_0}\ln 32 = 32R{T_0}\ln {2^5} = 160R{T_0}\ln 2 = 160{P_0}{V_0}\ln 2$$
Thus, the correct mapping is (S) $$\to$$ (1).
Comments (0)


