JEE Advance - Physics (2013 - Paper 2 Offline - No. 18)
A right-angled prism of refractive index $$\mu$$1 is placed in a rectangular block of refractive index $$\mu$$2, which is surrounded by a medium of refractive index $$\mu$$3, as shown in the figure. A ray of light e enters the rectangular block at normal incidence. Depending upon the relationships between $$\mu$$1, $$\mu$$2 and $$\mu$$3, it takes one of the four possible paths 'ef', 'eg', 'eh' or 'ei'.
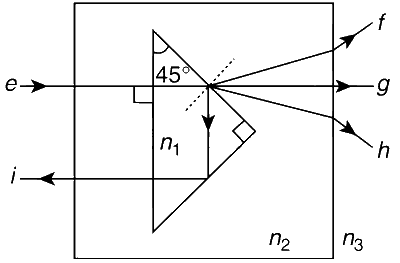
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:
| List I | List II | ||
|---|---|---|---|
| P. | $$e \to f$$ |
1. | $${\mu _1} > \sqrt 2 {\mu _2}$$ |
| Q. | $$e \to g$$ |
2. | $${\mu _2} > {\mu _1}$$ and $${\mu _2} > {\mu _3}$$ |
| R. | $$e \to h$$ |
3. | $${\mu _1} = {\mu _2}$$ |
| S. | $$e \to i$$ |
4. | $${\mu _2} < {\mu _1} < \sqrt 2 {\mu _2}$$ and $${\mu _2} > {\mu _3}$$ |
Explanation
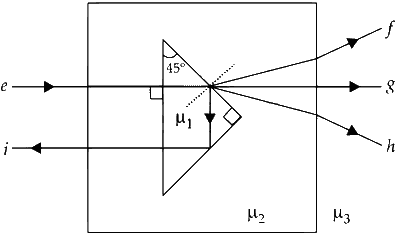
For e $$\to$$ f
$$\mu$$2 > $$\mu$$1, as ray bends towards the normal.
$$\mu$$2 > $$\mu$$3, as ray bends away from the normal.
P $$\to$$ 2
For e $$\to$$ g
$$\mu$$1 = $$\mu$$2 as there is no deviation.
Q $$\to$$ 3
For e $$\to$$ h
$$\mu$$2 < $$\mu$$1, as ray bends away from the normal.
$$\mu$$2 > $$\mu$$3, as ray bends away from the normal.
Also, $$\mu$$1 < $$\sqrt2$$$$\mu$$2 (No total internal reflection)
R $$\to$$ 4
For e $$\to$$ i
Total internal reflection takes place
$$\therefore$$ sin45$$^\circ$$ > sinC
But $$\sin C = {{{\mu _2}} \over {{\mu _1}}}$$
$$\therefore$$ $${1 \over {\sqrt 2 }} > {{{\mu _2}} \over {{\mu _1}}} \Rightarrow {\mu _1} > \sqrt 2 {\mu _2}$$
$$S \to 1$$
Comments (0)


