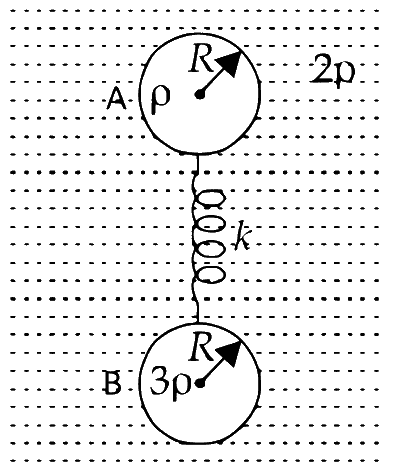
Considering FBDs of spheres A and B, we get

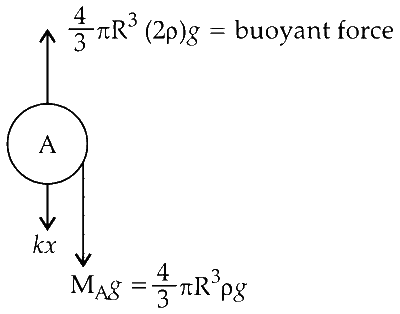
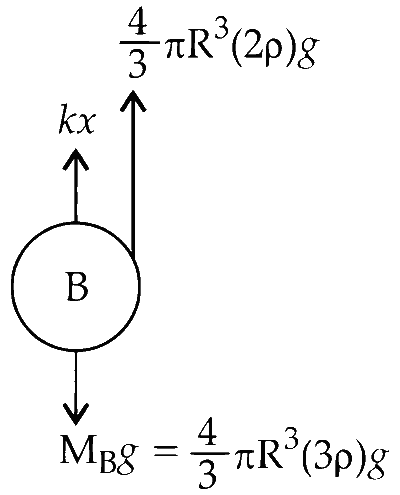
Here, $x$ is the extension produced in the spring

At equilibrium $\Sigma \mathrm{F}_{\mathrm{A}}=0$ and $\Sigma \mathrm{F}_{\mathrm{B}}=0$

$$ \begin{aligned} \frac{4}{3} \pi R^3(2 \rho) g & =k x+\frac{4}{3} \pi R^3 \rho g ...........(i)\\\\ k x+\frac{4}{3} \pi R^3(2 \rho) g & =\frac{4}{3} \pi R^3(3 \rho) g .........(ii)\end{aligned} $$

Subtract (ii) from (i), we get

$$ \begin{aligned} -k x & =k x-\frac{4}{3} \pi \mathrm{R}^3(2 \rho) g \\\\ x & =\frac{4 \pi \mathrm{R}^3 \rho g}{3 k} \end{aligned} $$

(Option A is correct)

If we consider both the spheres as a system, then at equilibrium,

$$ \begin{aligned} \text { total weight } & =\text { buoyant force } \\ \text { Total weight }(\mathrm{A}+\mathrm{B}) & =\frac{4}{3} \pi \mathrm{R}^3(4 \rho) g \\ \text { Total buoyant force } & =\frac{4}{3} \pi \mathrm{R}^3(4 \rho) g \end{aligned} $$

Hence, sphere A (light sphere) is completely submerged (option D is correct)