To determine the minimum velocity required for the bob of mass $ m $ to complete a full circle in the vertical plane, we start with the condition at the bottommost point:

$ u = \sqrt{5 g l_1} \text{ (at point A)} $

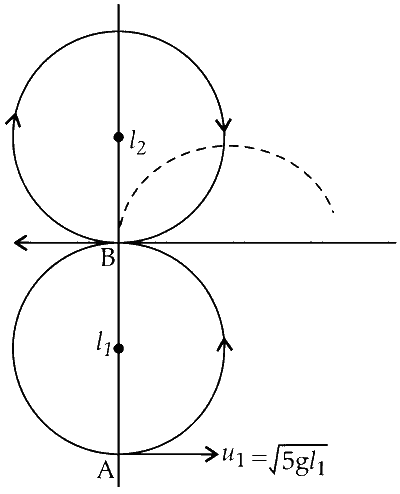
At the highest point B, using the conservation of energy, we get:

$ \frac{1}{2} m u_1^2 = m g (2 l_1) + \frac{1}{2} m v_1^2 $

Simplifying, we have:

$ v_1^2 = u_1^2 - 4 g l_1 $

Substituting $ u_1 = \sqrt{5 g l_1} $:

$ v_1^2 = 5 g l_1 - 4 g l_1 $

$ v_1 = \sqrt{g l_1} $

When the bob at point B elastically collides with another identical mass that is initially at rest, the velocities swap due to the nature of elastic collisions. Thus, the second bob attains the velocity:

$ u_2 = v_1 = \sqrt{g l_1} $

For the second bob to complete its circular path, the minimum velocity requirement is:

$ u_2 = \sqrt{5 g l_2} = \sqrt{g l_1} $